Визначення допустимих величин вільних членів умовних рівнянь.

Якість польових вимірів визначають обчисленням вільних членіів умовних рівнянь з встановленими для них допусками.

В загальному випадку граничну величину вільного члена умовного рівняння

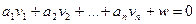, (6.23)

знаходять за формулою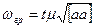

де m - середня квадратична похибка одиниці ваги,

t - параметр, який при заданій довірчій ймовірності залежить від кількості вимірів у мережі;

[аа] - сума квадратів коефіцієнтів умовного рівняння.

При зрівноваженні кутів похибку одиниці ваги беруть рівною середній квадратичній похибці виміряного кута для відповідного класу тріангуляції.

Середню квадратичну похибку виміряного кута обчислюють по нев'язкам трикутників

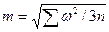
де 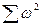- сума квадратів нев'язок трикутників;

n - кількість нев'язок трикутників.

Нев'язки трикутників обчислюють по кутам, приведеним до центра знаків

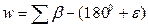- на сфері, (6.26)

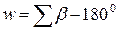- на площині, (6.27)

де 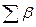- сума виміряних кутів в трикутнику;

e- сферичний надлишок трикутника.

Граничні нев'язки трикутників, обчислені за формулою

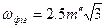
не повинні перевищувати 3, 4, 6 і 8" в тріангуляції 1, 2, 3 і 4 класів відповідно.

Вільні члени полюсних умов в геодезичних чотирикутниках і центральних системах повинні бути не більше

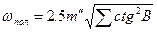
де 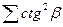- сума квадратів котангенсів зв'язуючих кутів трикутників;

m" - середня квадратична похибка вимірювання кутів.

Значення вільних членів базисного і азимутального умов не повинні перевищувати величини, обчислені за формулами:

для базисного умовного рівняння (в метрах)

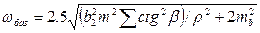
для азимутального умовного рівняння

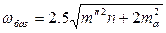
де 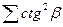- сума квадратів котангенсів зв'язуючих кутів трикутників;

b₂ - довжина базисної сторони на другому кінці ряду трикутників;

m_b, m_a та - середні квадратичні похибки базисних сторін і вихідних азимутів;

n - кількість кутів в передачі азимута.

Висновки

Якщо вільний член якого-небудь умовного рівняння не задовольняє встановленим допускам, то таке рівняння включати в зрівноваження мережі не можна до тих пір, поки не будуть виявлені і усунені причини, які призвели до недопустимої величини вільного члена даного умовного рівняння.

У виміряні кути слід ввести поправки за центрування та редукцію, за кривизну зображення геодезичної лінії на площині.

Вихідну сторону тріангуляції необхідно редукувати з еліпсоїда на площину в проекції Гаусса - Крюгера.

Контрольні запитання

1. Обґрунтувати формули для визначення елементів приведення.

2. Написати формулу поправки за центрування.

3. Написати формулу поправки за редукцію.

4. Привести формули поправки в напрямок за кривизну зображення геодезичної лінії на площині.

5. Обґрунтувати формули редукування довжини вихідної сторони з еліпсоїда на площину.

6. Обґрунтувати формулу зближення меридіанів.

7. Обґрунтувати формулу переходу від геодезичного азимуту до дирекційного кута.