Дифференциальные уравнения, приводящиеся к однородным
Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут быть приведены к однородным.
Это уравнения имеют вид 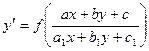 .
.
Если определитель 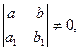 то переменные могут быть разделены подстановкой
то переменные могут быть разделены подстановкой
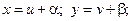
где 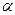 и
и 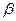 - решения системы уравнений
- решения системы уравнений 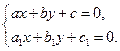
Пример. Решить уравнение 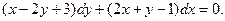
Имеем
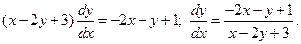
Находим значение определителя 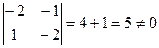 .
.
Решаем систему уравнений 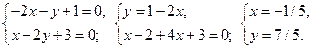
В исходном уравнении сделаем подстановку: 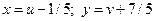 . Получим:
. Получим:
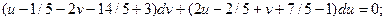
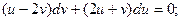
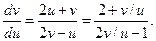
Заменяя переменную 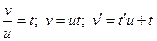 при подстановке в выражение, записанное выше, будем иметь:
при подстановке в выражение, записанное выше, будем иметь:
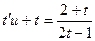 ;
;
Разделяя переменные получим:
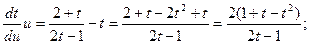
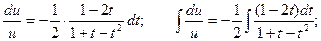
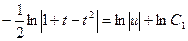 ;
; 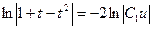 ;
;
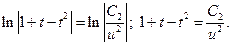
Переходим к первоначальной функции у и переменной х:
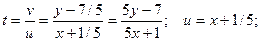
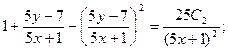
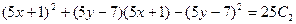 ;
;
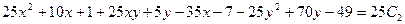 ;
;
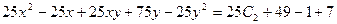 ;
;
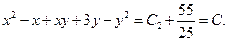
Таким образом, выражение 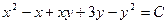 является общим интегралом исходного дифференциального уравнения.
является общим интегралом исходного дифференциального уравнения.
В случае если в исходном уравнении вида 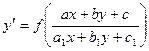 определитель
определитель 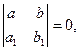 то переменные могут быть разделены подстановкой
то переменные могут быть разделены подстановкой
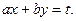
Пример. Решить уравнение 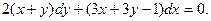
Получаем 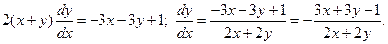
Находим значение определителя 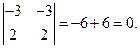
Применяем подстановку 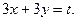 Получим
Получим
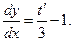
Подставляя это выражение в исходное уравнение будем иметь:
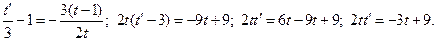
Разделяя переменные получим:
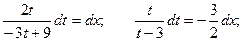
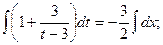
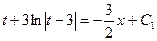
Возвращаясь к первоначальной функции у и переменной х, находим
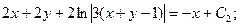
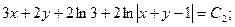
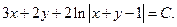
Таким образом, получили общий интеграл исходного дифференциального уравнения.
Дата добавления: 2016-05-05; просмотров: 614;
