Закон радиоактивного распада

Количество любых радионуклидов со временем уменьшается вследствие радиоактивного распада. Особенность радиоактивного распада состоит и в том, что нуклиды одного и того же элемента распадаются не все сразу, а постепенно, в различное время. Каждое ядро обязательно распадется, только момент распада конкретного ядра предсказать невозможно. Можно лишь указать, что за определенный промежуток времени распадется такое-то количество радионуклидов. Поэтому говорят, что радиоактивный распад носит вероятностный характер.

Скорость распада определяется строением ядра, и поэтому на этот процесс невозможно повлиять никакими обычными физическими или химическими способами.

Кроме того, если мы будем наблюдать за малым количеством радионуклидов (например, 5 или 25 нуклидов), то мы не заметим никаких закономерностей радиоактивного распада. Малое число ядер может распасться сразу в момент начала наблюдения, а может не распадаться довольно большое время, или распад может идти неравномерно: то большими, то меньшими порциями. Закономерности распада проявляются для большого числа радионуклидов, как правило, более чем 100 ядер. Такие закономерности, характерные для большого количества данных, описываются математически с помощью статистики. Исходя из этого говорят, что радиоактивный распад носит статистический характер, т. е. справедлив для большого количества нуклидов.

Все указанные выше особенности радиоактивного распада позволяют определить его как статистический вероятностный процесс, т.е. вероятность распада для данного радионуклида постоянна и не зависит от присутствия или отсутствия других радиоактивных ядер. Скорость распада зависит только от числа радиоактивных ядер в данный момент вре­мени. Такие процессы описываются экспоненциальным соотношением. Мате­матически закон радиоактивного распада выражается следующим уравнением и устанавливает, что за единицу времени распадается всегда одна и та же доля имеющихся в наличии ядер:

N_t = N₀×e^-lt,

где N_t – количество атомных ядер, оставшихся через промежуток вре­мени t; N₀ – начальное количество атомных ядер, т. е. количество ядер в момент наблюдения при t =0; е = 2,72 - основание натурального логарифма, которое указывает на графический вид математической зависимости (графически распад выражается не прямой линией, а экспонентой); l - постоянная радиоактивного распада, показывающая какая доля радионуклидов распадается в единицу времени; t – время распада.

Постоянная радиоактивного распада является справочной величиной и строго определенной для каждого типа радионуклидов; она также характеризует относительную скорость распада. Размерность постоянной распада выражают в обратных единицах времени: с^-1, мин^-1, ч^-1 и т. д., чтобы показать, что количество радионуклидов не растет, а убывает. Величину, обратную постоянной радиоактивного распада t = 1/l, называют средней продолжительностью жизни ядра.

Графически закон радиоактивного распада выражается экспоненциаль­ной кривой (рис. 1).

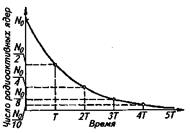
Рис.1. Кривая радиоактивного распада.

Для характеристики скорости распада радиоактивных элементов в прак­тике пользуются вместо постоянной распада периодом полураспада.

Период полураспада– это время, в течение которого распадается поло­вина исходного количества радиоактивных ядер. Он обозначается буквой Т_1/2 и выражается в единицах времени. Для различных радиоактивных изотопов пе­риод полураспада имеет значения от долей секунды до миллиардов лет. причем у одного и того же элемента могут быть изотопы с различными периодами полураспада. По­этому радиоактивные изотопы разделяются на короткоживущие (часы, дни) и долгоживущие (годы). Период полураспада, также как и постоянная распада, является ядерной постоянной, строго определенной для каждого типа радионуклидов и справочной величиной. Только случайно два периода полураспада могут оказаться одинаковыми или очень близкими для того, чтобы их можно было отличить. Так, марганец-56 и никель-65 имеют периоды полураспада 2,58 и 2,56 ч соответственно.

Зная период полураспада или постоянную распада, всегда можно произвести идентификацию радионуклида, т. е. указать, какой именно радионуклид присутствует в данном образце или продукте. Период полураспада связан с постоянной радиоактивного распада соотношением:

l = 0,693/Т_1/2 или Т_1/2 = 0,693/l.

Это соотношение показывает, что между этими двумя постоянными существует обратная зависимость, т. е. чем больше значение l, тем меньше величина Т_1/2 и, соответственно, распад протекает быстрее; и, наоборот, чем меньше l, тем больше Т_1/2 и распад идет медленнее. Заменив l в формуле на Т_1/2, получим

N_t = N₀×e^-0,693t/Т

Чтобы узнать полное время жизни данных радионуклидов, необходимо увеличить Т_1/2 в 10 раз. Например, у стронция-90 Т_1/2 » 29 лет, следовательно, через 290 лет данный искусственный радионуклид практически полностью распадется с момента его образования. Однако, исходя из вида экспоненциальной кривой, которая всегда стремится к нулю, но его не достигает, всегда есть вероятность, что хотя бы мизерное количество данных радионуклидов может через 10Т_1/2 не распасться.

Радиоактивное превращение одного из ядер никак не влияет на пре­вращение соседних ядер, т.е. процессы распада различных ядер протекают абсолютно независимо друг от друга. Радиоактивный распад нельзя замедлить или ускорить действием температуры, давления, изменением химического состояния ато­мов или каким-либо другим способом. Поэтому, в отличие от химических от­равляющих веществ, радиоактивные вещества нельзя обезопасить ни какой-либо химической реакцией, ни физической обработкой.

Также бессмысленно говорить о времени полураспада или времени жизни одного радиоактивного ядра. При использовании этих терминов подразумевают усредненные величины, справедливые при наличии достаточного большого числа ядер данного изотопа. Когда говорят о среднем времени жизни радиоактивного ядра, то понимают под этим среднее время жизни ядер в каком-либо образце, содержащем эти радиоактивные ядра.