Дифференциальное уравнение движения идеальной жидкости. Уравнение Эйлера.

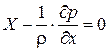
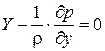
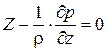
В этом случае воспользуемся принципом Даламбера: "всякое движение можно рассматривать как равновесие, если к нему добавить силы инерции"

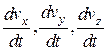- ускорения в проекциях

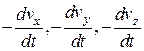- единичные массовые силы в проекциях

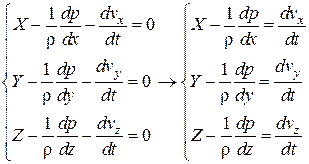система дифференциальных уравнений идеальной жидкости (уравнения Эйлера)

Полное ускорение в направлении оси координат складывается из ускорений. Вызванных массовыми силами и силами давления.

Эти уравнения справедливы для сжимаемых и несжимаемых жидкостей, для установившегося и неустановившегося движения.

Уравнение Бернулли для элементарной струйки идеальной жидкости.

Для элементарной струйки идеальной жидкости запишем систему дифференциальных уравнений движения жидкости:

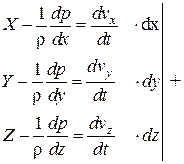
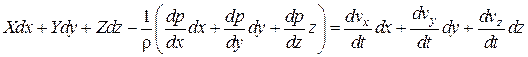
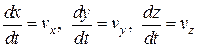
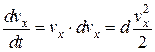
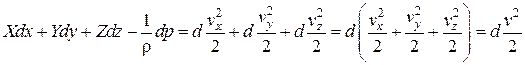
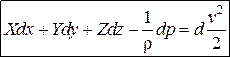уравнение элементарной струйки идеальной жидкости

Рассмотрим это уравнение в поле сил тяжести: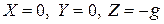

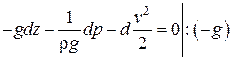
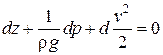
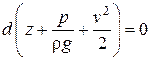
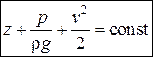
Для любых двух живых сечений элементарной струйки можно записать: 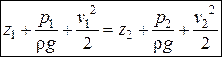уравнение Бернулли для элементарной струйки идеальной жидкости.