Tneр— и Тпер Т*2 fnep •уо

Необходимо напомнить, что в первую очередь судоводитель дол­жен определить основные обстоятельства встречи, т. е. D_Kp и f_Kp, а за­тем уже определять элементы движения цели.

Истинное перемещение цели является суммой двух_перемещений — относительного 5₀(Р₀) ^и судна-наблюдателя 5_Н(Р_Н): £ц = £о+8_Н или Vц = ^о“Ь Рн- _ ^

Учитывая коммутативность суммы векторов (So+Sh = Sh+<>o), можно находить 5_Ц (Г_ц) двумя способами.

Построение векторного треугольника (см. рис. 19.2), показанное сплошными линиями, называется прямым. При нем начала векторов скоростей (линий путей), проложенных в сторону движения судов, на­ходятся в одной точке.

Применяется иногда также обратное построение, при котором векторы, откладываемые в сторону движения судов, сходятся своими концами в общую точку (показаны пунктиром).

В дальнейшем мы будем в основном пользоваться прямым постро­ением, так как оно более удобно при решении задач расхождения.

Длина вектора движения судна-наблюдателя должна быть равна в выбранном масштабе плаванию своего судна за время между на­блюдениями, принятыми для построения векторного треугольника. Длина полученного вектора движения цели соответствует плаванию цели за время между наблюдениями.

Относительная прокладка выполняется на радиолокационном ма­невренном планшете, представляющем собой сетку полярных коор­динат. Для ускорения расчетов, связанных с плаванием судна за вре­мя между наблюдениями, на маневренном планшете помещена лога­рифмическая шкала. На практике для ускорения прокладки использу­ют следующие приемы, исключающие необходимость использования логарифмической шкалы.

1. Независимо от интервала времени между наблюдениями век­торный треугольник строят за промежуток времени б мин. В этом слу­чае длина каждого вектора составляет */ю соответствующей скорости.

2. Экстраполированные позиции цели находят откладыванием по ЛОД расстояния между двумя известными ее позициями.

3. Сразу после получения первого положения цели в ее точку на­правляют вектор в масштабе 1:10. После получения второго по­ложения цели находят экстраполяцией ее положение через 6 мин после первого наблюдения (если ЫФ6 мин) и из начала вектора Г„ в эту точку проводят вектор Р_ц.

4. *_Кр и ^ер рассчитывают, откладывая по ЛОД отрезки, равные Vo. и деля глазомерно отрезок, включающий точку кратчайшего сбли­жения или точку пересечения курса.

			Рис. 19.4. Влияние погрешностей в позиции цели на радиолокационную прокладку

На рис. 19.3 показаны построения по двум позициям цели, полу­ченным с интервалом 3 мин.

При проведении ЛОД через две точки цели возможны ошибки в оценке ситуации, связанные с промахом в нанесении одной из пози­ций или маневром цели в промежутке между наблюдениями. Для иск­лючения этих ошибок следует по возможности .иметь для первоначаль­ной оценки ситуации три позиции каждой цели.

Точность определения обстоятельств встречи и элементов движения судов. При обработке радиолокационных наблюдений следует иметь в виду, что обстоятельства встречи, курс и скорость цели определяют­ся с погрешностями, которые в ряде случаев могут быть весьма зна­чительными. Особенно важно учитывать вероятную погрешность в D_Kp при оценке опасности столкновения.

Проведенные исследования показали, что при работе на шкалах среднего масштаба (15—16 миль) вследствие погрешности измерения пеленгов и дистанций относительное положение цели находится со средней квадратической погрешностью М«0,6 кб. Если суммарную по­грешность в двух относительных позициях цели отнести (точки / и 2 на рис. 19.4) ко второму моменту наблюдения, можно считать, что второе относительное положение определено с суммарной погрешно­стью М _£ «0,85 кб.

Погрешность в определении позиции цели в первую очередь при­водит к погрешности определения D_KV (см. рис. 19.4):

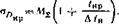
(19.1)

Значения средней квадратической погрешности определения D_KР в зависимости от и промежутка времени между наблюдениями Д/_н приведены на графике (рис. 19.5).

С вероятностью р=0,95 предполагаемая дистанция расхождения судов лежит в пределах D_Kp=rt2ar _кр. Погрешности в определении D_Кр весьма существенны и должны обязательно учитываться при оцен­ке опасности сближения.

Как видно из рис. 19.4, вследствие погрешности в определении по­зиции цели возникают погрешности в определении t_KР, /С_ц и У_ц.

Рис. 19.5. Средняя квадратическая Рис. 19.6. Средняя квадратическая по-