ЛЕКЦИЯ 5. Преобразование уравнений.

1. Методы линеаризации нелинейных уравнений.

2. Преобразование дифференциальных уравнений к операторному.

1. Методы линеаризации нелинейных уравнений.

Решение систем линейных уравнений- задача, к решению которой хорошо приспособлены аналоговые вычислительные машины.

Нелинейность резко усложняет решение, и, как правило, в этом случае требуется использование численных методов.

Часто применяется метод линеаризации нелинейных уравнений. Для линеаризации нелинейной функции необходимо ее разложить в ряд Тейлора или Маклорена.

Производная функции определяется разностным отношением:

.

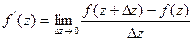Если существует предел и не зависит от того, как стремится к нулю, то функция является аналитической. Следовательно в окрестности некоторой точки а можно ее разложить в ряд Тейлора:

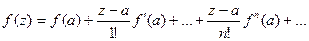
Если а=0 , то получаем ряд Маклорена:

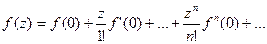
Учитывая , что последующие слагаемые выше второго достаточно малые величины, можно заменить функцию линейной частью разложения.

2. Преобразование дифференциальных уравнений к операторному

Результаты моделирования динамических процессов часто сводится к решению дифференциальных уравнений. Если применить к дифференциальным уравнениям операционные исчисления, то облегчается решение дифференциальных уравнений.

К операторным методам относится метод преобразования Лапласа:

.

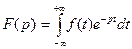Обратное преобразование имеет вид:

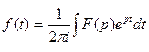
F(p)=L[f(t)] – называется изображением функции f(t), называемой оригиналом.

Основные свойства преобразования Лапласа:

1. Линейность

L[f₁(t)+f₂(t)]=L[f₁(t)]+L[f₂(t)]=F₁(p)+F₂(p)

L[af(t)]=aL[f(t)]=aF(p)

2. Свойство подобия

L[f(at)]=1/a F(p/a)

3. Правило дифференцирования

L[df/dt]=pF(p)-f₀

L[d²f/dt²]=pF(p)-(pf₀+f₁)

4. Правило интегрирования

L[∫f(t)dt]= F(p)/p +(f-1)/p

L[ ∫∫ f(t) (dt)² ]= F(p)/p² + (f-1)/p² +(f-2)/p

5. Теорема о предельном значении

lim f(t) = lim p F(p)

t→0 p→0

1. Теорема о начальном значении

lim f(t) = lim F(p)

t→0 p→∞

1. Теорема о запаздывания

L [ f(t-τ) ] =e^-τp F(p)

1. Теорема о сдвиге

L [ e ^{± λ t} f(t) ]= F(p ±λ)

1. Теорема о свертке

Если F₁(p)= L[ f₁ (t) ] и F₂(p)= L[ f₂ (t) ] , то

F₁ (p) F₂ (p)= L [ ∫ f₁ (t- τ) f₂ (τ) dt ]