Линейный коэффициент корреляции

Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон. Коэффициент корреляции рассчитывается по формуле:

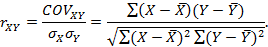
Коэффициент корреляции изменяется в пределах от минус единицы до единицы^[11].

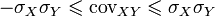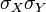Разделив обе части двойного неравенства на получим

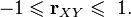
Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: 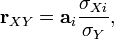где 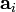— коэффициент регрессии, 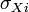— среднеквадратическое отклонение соответствующего факторного признака^[12].

Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».

Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений).

Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или 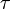(тау) Кендалла.

В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция.

Билет 6

Классы. Отношения между классами

Класс — разновидность абстрактного типа данных в (ООП), характеризуемый способом своего построения.

Суть отличия классов от других абстрактных типов данных состоит в том, что при задании типа данных класс определяет одновременно и интерфейс, и реализацию для всех своих экземпляров.

представление некоторого количества классов и связей между ними называется диаграммой классов.