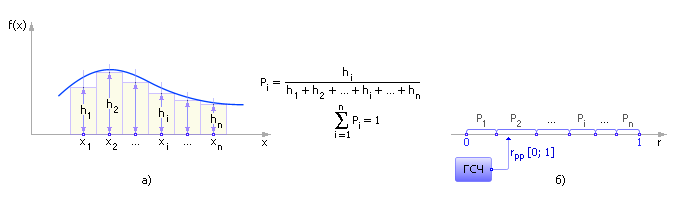Метод ступенчатой аппроксимации

Необходимо уметь превращать равномерный ГСЧ в генератор случайных чисел с заданным произвольным законом распределения.

Обозначим: h_i — высота i-го столбца, f(x) — распределение вероятности (показывает насколько вероятно некоторое событие x). Значение h_i операцией нормировки необходимо перевести в единицы вероятности появления значений x из интервала x_i < x ≤ x_{i + 1}: P_i = h_i/(h₁ + h₂ + … + h_i + … + h_n).

Операция нормировки обеспечивает сумму вероятностей всех n событий равную 1:

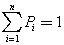
На рис. 24.2 показаны графически переход от произвольного непрерывного закона распределения к дискретному (рис. 24.2, а), отображение получаемых вероятностей на интервал r_рр[0; 1] и генерация случайных событий с использованием эталонного равномерно распределенного ГСЧ (рис. 24.2, б).

Рис. 24.2. Иллюстрация метода ступенчатой аппроксимации

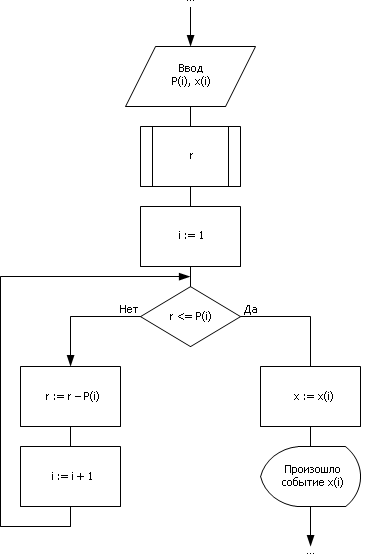
На рис. 24.3 показан фрагмент алгоритма, реализующего описанный метод. Алгоритм генерирует случайное число, равномерно распределенное от 0 до 1. Затем, сравнивая границы отрезков, расположенных на интервале от 0 до 1, представляющих собой вероятности P выпадения тех или иных случайных величин X, определяет в цикле, какое из случайных событий i в результате этого выпадает.

Рис. 24.3. Блок-схема алгоритма, реализующего метод ступенчатой аппроксимации

Метод усечения

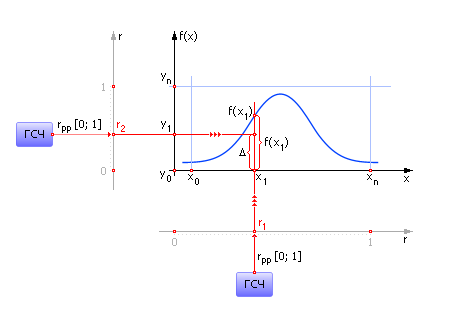
Метод используется в случае, когда функция задана аналитически (в виде формулы). График функции вписывают в прямоугольник (см. рис. 24.4).

На ось Y подают случайное равномерно распределенное число из ГСЧ.

На ось X подают случайное равномерно распределенное число из ГСЧ. Если точка в пересечении этих двух координат лежит ниже кривой плотности вероятности, то событие X произошло, иначе нет.

Недостатком метода является то, что те точки, которые оказались выше кривой распределения плотности вероятности, отбрасываются как ненужные, и время, затраченное на их вычисление, оказывается напрасным.

Рис. 24.4. Иллюстрация метода усечения