Неразрешимость проблемы останова

Проблема останова для машины Тьюринга формулируется следующим образом: можно ли определить по данной машине Тьюринга в произвольной конфигурации со строкой конечной длины непустых символов на ленте остановится ли она? Говорят, что эта проблема рекурсивно неразрешима, что означает, что не существует алгоритма, который для любой Tm в произвольной конфигурации определял бы остановится ли в конце концов Tm.

Перенумеруем все машины Тьюринга и все возможные входы над алфавитом 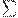. Рассмотрим язык

L₁={x_i|x_i не допускается T_i}

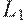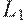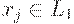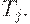Ясно, что не допускается никакой Tm. Допустим, что это не так. Пусть допускается Tj. Тогда тогда и только тогда, когда не допускается Но поскольку допускает тогда и только тогда, когда допускается 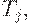- противоречие. Так что 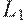- не является рекурсивно перечислимым множеством.

Предположим, что мы имеем алгоритм (то есть машину Тьюринга, которая всегда останавливается) для определения, остановится ли машина Тьюринга в данной конфигурации. Тогда следующим образом можно построить машину Тьюринга T, допускающую .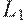

1. Если дано слово x, T перечисляет слова x₁, x₂... пока не будет x_i = x.

2. T генерирует кодировку машины Тьюринга T_i.

3. Управление передается гипотетической машине, которая определяет останавливается ли T_i на входе x_i.

4. Если выясняется, что T_i не останавливается на входе x_i, то T останавливается и допускает x_i.

5. Если выясняется, что T_i останавливается на входе x_i, то управление передается универсальной машине Тьюринга, которая моделирует T_i на входе x_i. Поскольку T_i в конце концов останавливается, универсальная машина Тьюринга в конце концов останавливается и определяет допускает ли T_i слово x_i.

В любом случае T останавливается, допуская x_i в том случае, когда T_i отвергает x_i, и отвергая x_i, когда T_i допускаетx_i.

Таким образом, из нашего предположения, что существует машина Тьюринга, которая определяет, останавливается ли произвольная машина Тьюринга, следует, что L₁ допускается некоторой машиной Тьюринга, а это противоречит доказанному выше. Это, в свою очередь, дает теорему:

Теорема 2.2. Не существует алгоритма для определения того, остановится ли произвольная машина Тьюринга в произвольной конфигурации.