Типы грамматик и их свойства
Рассмотрим классификацию грамматик (предложенную Н.Хомским), основанную на виде их правил.
Определение. Пусть дана грамматика G = (N, T, P, S). Тогда
(1) если правила грамматики не удовлетворяют никаким ограничениям, то ее называют грамматикой типа 0, или грамматикой без ограничений.
(2) если
1. каждое правило грамматики, кроме 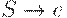 , имеет вид
, имеет вид  , где
, где 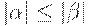 , и
, и
2. в том случае, когда 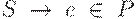 , символ S не встречается в правых частях правил, то грамматику называют грамматикой типа 1, или неукорачивающей или контекстно-зависимой (КЗ- грамматикой) или контекстно - чувствительной (КЧ- грамматикой).
, символ S не встречается в правых частях правил, то грамматику называют грамматикой типа 1, или неукорачивающей или контекстно-зависимой (КЗ- грамматикой) или контекстно - чувствительной (КЧ- грамматикой).
(3) если каждое правило грамматики имеет вид 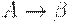 , где
, где 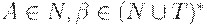 , то ее называют грамматикой типа 2, или контекстно-свободной (КС-грамматикой).
, то ее называют грамматикой типа 2, или контекстно-свободной (КС-грамматикой).
(4) если каждое правило грамматики имеет вид либо 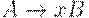 , либо
, либо 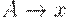 , где
, где 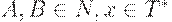 то ее называют грамматикой типа 3, или праволинейной.
то ее называют грамматикой типа 3, или праволинейной.
Легко видеть, что грамматика в примере 2.5 - неукорачивающая, в примере 2.6 - контекстно-свободная, в примере 2.7 - праволинейная.
Язык, порождаемый грамматикой типа i, называют языком типа i. Язык типа 0 называют также языком без ограничений, язык типа 1 - контекстно-зависимым (КЗ), язык типа 2 - контекстно-свободным (КС), язык типа 3 - праволинейным.
Теорема 2.1. Каждый контекстно-свободный язык может быть порожден неукорачивающей контекстно- свободной грамматикой.
Доказательство. Пусть L - контекстно-свободный язык. Тогда существует контекстно-свободная грамматика G = (N, T, P, S), порождающая L.
Построим новую грамматику G' = (N',T,P',S') следующим образом:
1. Если в P есть правило вида 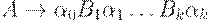 , где
, где 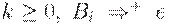 для
для 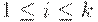 и ни из одной цепочки
и ни из одной цепочки 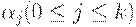 не выводится e, то включить в P' все правила (кроме
не выводится e, то включить в P' все правила (кроме 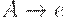 ) вида
) вида
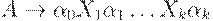
где 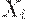 это либо
это либо 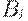 , либо e.
, либо e.
2. Если 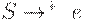 , то включить в P' правила
, то включить в P' правила 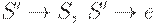 и положить
и положить  . В противном случае положить
. В противном случае положить 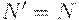 и
и 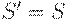 . Порождает ли грамматика пустую цепочку можно установить следующим простым алгоритмом:
. Порождает ли грамматика пустую цепочку можно установить следующим простым алгоритмом:
Шаг 1. Строим множество 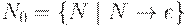
Шаг 2. Строим множество 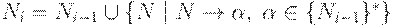
Шаг 3. Если 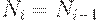 , перейти к шагу 4, иначе шаг 2.
, перейти к шагу 4, иначе шаг 2.
Шаг 4. Если 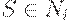 , значит
, значит 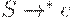 .
.
Легко видеть, что 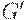 - неукорачивающая грамматика. Можно показать по индукции, что
- неукорачивающая грамматика. Можно показать по индукции, что  .
.
Пусть Ki - класс всех языков типа i. Доказано, что справедливо следующее (строгое) включение: 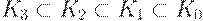 .
.
Заметим, что если язык порождается некоторой грамматикой, это не означает, что он не может быть порожден грамматикой с более сильными ограничениями на правила. Приводимый ниже пример иллюстрирует этот факт.
Пример 2.8. Рассмотрим грамматику 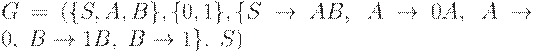 . Эта грамматика является контекстно-свободной. Легко показать, что
. Эта грамматика является контекстно-свободной. Легко показать, что  . Однако, в примере 2.7 приведена праволинейная грамматика, порождающая тот же язык.
. Однако, в примере 2.7 приведена праволинейная грамматика, порождающая тот же язык.
Ниже приводятся подробные примеры решения двух практически интересных более сложных задач на построение КС- и НС-грамматик.
Пример 2.9. Данный пример относится к несколько парадоксальной для грамматик постановке: построить КС-грамматику, порождающую язык:
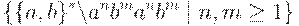
т.е. построить все цепочки кроме указанных (обычно-то говорят о том, что надо построить). Но, может быть, в такой постановке заложена и подсказка к решению? Известно, что иные задачи с подобными требованиями так и решаются: нужно сделать все, "что не надо", а потом отклониться от этого "не надо" всеми возможными способами.
Однако воодушевлнных построением в рамках КС- грамматики цепочек вида 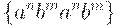 (здесь и далее в этом примере
(здесь и далее в этом примере 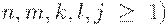 ждет некоторое разочарование. Действительно, в отличие от таких случаев, как
ждет некоторое разочарование. Действительно, в отличие от таких случаев, как 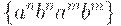 ,
, 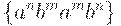 ,
, 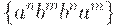 и т.п., обе зависимости (по n и по m ) придется отслеживать одновременно и из двух разных центров порождения, к чему КС-грамматики по своей природе (виду своих правил) оказываются не предназначены.
и т.п., обе зависимости (по n и по m ) придется отслеживать одновременно и из двух разных центров порождения, к чему КС-грамматики по своей природе (виду своих правил) оказываются не предназначены.
Попробуем тогда пересказать условие задачи в конструктивном (созидательном) плане, т.е. обозначая лишь то, что нам нужнопостроить, а не наоборот. Поначалу такое множество цепочек кажется необозримым. Но попробуем, "Дорогу осилит идущий"! Начнем с очевидных случаев:
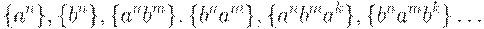
Однако бесконечно продолжать в духе 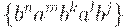 уже как- то скучно. Замечаем, что
уже как- то скучно. Замечаем, что 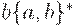 вполне конечным образом определяет половину из упомянутых бесчисленных описаний, а в следующий момент симметрия нам подсказывает и язык
вполне конечным образом определяет половину из упомянутых бесчисленных описаний, а в следующий момент симметрия нам подсказывает и язык 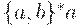 .
.
Таким образом, все цепочки вышеперечисленных видов укладываются в три случая:
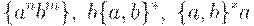
Далее рассмотрим случай 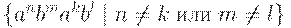 . Но что такое, к примеру,
. Но что такое, к примеру, 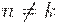 ? То же самое, что объединение условий
? То же самое, что объединение условий  ! И здесь перешли к конструктиву, который несложно строится в рамках КС-грамматики.
! И здесь перешли к конструктиву, который несложно строится в рамках КС-грамматики.
Остается единственный неупомянутый случай:
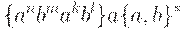
Вспоминая, что объединение КС-языков есть КС-язык, получаем искомое решение задачи.
Так, если язык 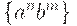 может быть порожден грамматикой
может быть порожден грамматикой
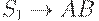
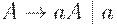
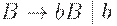
а язык 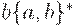 - грамматикой
- грамматикой
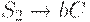
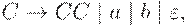
то для объединения этих языков (в общем случае использующих каждый свой уникальный набор вспомогательных знаков) достаточно добавить правило старта из новой общей аксиомы:
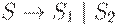
Пример 2.10. Построение НС-грамматики.
Грамматики непосредственных составляющих (или, кратко, НС-грамматики) есть вид представления контекстно-зависимых грамматик, т.е. они обладают теми же выразительными возможностями, что и КЗ-грамматики в целом. Каждое правило НС-грамматики должно соответствовать виду:
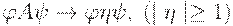
то есть левое и правое окружение (контекст) заменяемого знака A должны сохраниться и вокруг непустой заменяющей цепочки 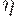 (греческая буква "эта".
(греческая буква "эта".
Такое дополнительное ограничение позволяет удобнее переходить от КЗ-грамматики к соответствующему линейно- ограниченному автомату
Рассмотрим построение НС-грамматики для языка
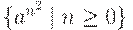 , порождающего слова вида
, порождающего слова вида 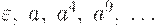
Для большей ясности сперва построим для этого языка грамматику общего вида, а потом перестроим ее в соответствии с НС-ограничениями.
Сам алгоритм порождения 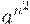 может основываться как на известном свойстве квадратов чисел, разность между соседними из которых образуют арифметическую прогрессию, так и на собственно "квадратности" интересующих чисел, т.е. того, что каждое квадратное число представимо наподобие матрицы из n строк и n столбцов единичных элементов (в связи с чем Пифагор и дал название подобным числам - квадратные, а среди других чисел по тому же принципу отметил треугольные, кубические, пирамидальные и т.п.). Последний подход представляется более общим, поскольку подобным образом мы сможем построить и
может основываться как на известном свойстве квадратов чисел, разность между соседними из которых образуют арифметическую прогрессию, так и на собственно "квадратности" интересующих чисел, т.е. того, что каждое квадратное число представимо наподобие матрицы из n строк и n столбцов единичных элементов (в связи с чем Пифагор и дал название подобным числам - квадратные, а среди других чисел по тому же принципу отметил треугольные, кубические, пирамидальные и т.п.). Последний подход представляется более общим, поскольку подобным образом мы сможем построить и 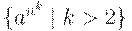 .
.
Итак, порождаем две группы по n элементов
| Правила | Вид получаемой цепочки |
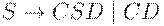
| 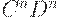
|
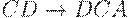
|  (A задерживает C) (A задерживает C)
|
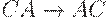
| 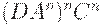 (отработали все C) (отработали все C)
|
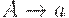
| 
|
Получили  но что делать с C и D? Сделав свое дело, они стали лишними.
но что делать с C и D? Сделав свое дело, они стали лишними.
В грамматике общего вида такие знаки сокращают ("увольняют"), а в КЗ-грамматиках - "переводят на другую работу" (в основные знаки). Но если мы просто напишем 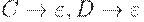 , вывод в случайный момент времени может закончиться досрочно и станет возможным порождение лишних цепочек.
, вывод в случайный момент времени может закончиться досрочно и станет возможным порождение лишних цепочек.
Поэтому в обоих случаях не обойтись без дальнейшего уточнения предназначения (миссий) и состава "действующих лиц". Отметим для этого самый первый из команды знаков C (назовем его B ) и самый последний из D (обозначим его E ). Когда B и Eвстретятся, это и будет признаком полного завершения процесса порождения знаков a.
Начнем вывод с начала:
| Правила | Вид получаемой цепочки |

| 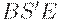
|
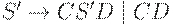
| 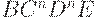
|
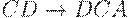
| 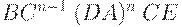 ( C прошло первый раз) ( C прошло первый раз)
|
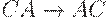
| 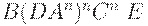 (прошли все C) (прошли все C)
|

| 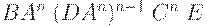
|
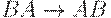
| 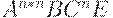 (ушли все D) (ушли все D)
|
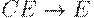
| 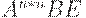 (ушли все C) (ушли все C)
|
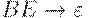
| 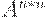 (ушли B c E) (ушли B c E)
|
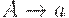
| 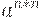
|
Результат получили, но какой ценой (для B, C, D и E )? Прямо-таки сталинские методы. Точнее скажем, в военных или иных чрезвычайных условиях иначе, порой, и нет возможности поступить. А в более мирное время? Попробуем "соблюдать КЗОТ" и обойтись без сокращений.
Снова:
| Правила | Вид получаемой цепочки |
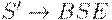
| 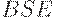
|
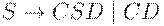
| 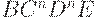
|
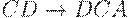
| 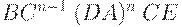 ( C прошло первое C ) ( C прошло первое C )
|
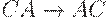
| 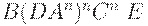 (прошли все C) (прошли все C)
|

| 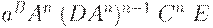
|
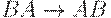
| 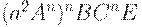 (ушли все D) (ушли все D)
|
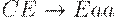
| 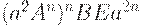 (ушли все C) (ушли все C)
|
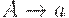
| 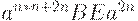 (ушли B c E) (ушли B c E)
|
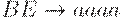
| 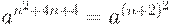
|
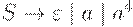
| 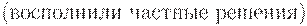
|
Итак, если сокращать нельзя, достраиваем слово до ближайшего подходящего квадрата. В данном случае удобнее достроить слово до 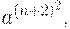 т.к. для достройки до
т.к. для достройки до 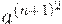 нам бы потребовалось перевести
нам бы потребовалось перевести 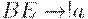 , т.е. опять что-то сократить. Напомним, что в КЗ-грамматиках допускается переход аксиомы в пустую цепочку (
, т.е. опять что-то сократить. Напомним, что в КЗ-грамматиках допускается переход аксиомы в пустую цепочку (  ), если аксиома нигде более не встречается в правых частях правил (т.е. когда из начального ничего получают другое ничего).
), если аксиома нигде более не встречается в правых частях правил (т.е. когда из начального ничего получают другое ничего).
Мы получили несокращающую грамматику. Но широко используемые при ее построении правила вида 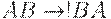 (
(  и т.п.), очевидно, не подходят под определение НС-грамматики (убедитесь!). Такие "рокировки" , однако, легко раскрыть через цепочку правил вида
и т.п.), очевидно, не подходят под определение НС-грамматики (убедитесь!). Такие "рокировки" , однако, легко раскрыть через цепочку правил вида
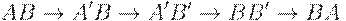
где 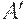 и
и 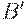 - нигде более в грамматике не используемые вспомогательные знаки. Отметим, что замену на промежуточные знаки и обратно на исходные нужно осуществлять в одном и том же порядке (слева-направо или, наоборот, только справа-налево), иначе в общем случае (когда назначение A и B в грамматике различно) возникают лишние цепочки.
- нигде более в грамматике не используемые вспомогательные знаки. Отметим, что замену на промежуточные знаки и обратно на исходные нужно осуществлять в одном и том же порядке (слева-направо или, наоборот, только справа-налево), иначе в общем случае (когда назначение A и B в грамматике различно) возникают лишние цепочки.
Так, применение замены
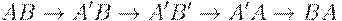
(нарушен порядок замен) при наличии соответствующего прово- кационного окружения допускает подмену B на A:

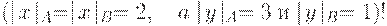
Замена AB на BA в рамках НС-грамматики коротко обозначается, как и обычный вывод: 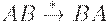 .
.
Таким образом, один из возможных наборов правил искомой НС-грамматики имеет следующий вид:
| Правила | Вид получаемой цепочки |
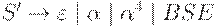
| BSE |
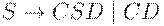
| BCnDn E |
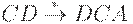
| BCn-1DCADn-1E |
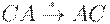
| BCn-1(DA)nCE |
| B(DAn)nCnE | |

| a2BAn(DAn)n-1CnE |
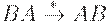
| (a2An)nBCnE |

| (a2An)nBEa2n |
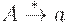
| an*n+2nBEa2n |
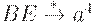
| 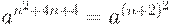
|
Машины Тьюринга
Формально машина Тьюринга ( Tm ) - это 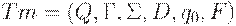 , где
, где
Q - конечное множество состояний;
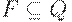 - множество заключительных состояний;
- множество заключительных состояний;
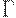 - множество допустимых ленточных символов; один из них, обычно обозначаемый B, - пустой символ
- множество допустимых ленточных символов; один из них, обычно обозначаемый B, - пустой символ
 - множество входных символов, подмножество \Gamma, не включающее B,
- множество входных символов, подмножество \Gamma, не включающее B,
D функция переходов, отображение из 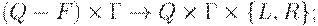 для некоторых аргументов функцияD может быть не определена.
для некоторых аргументов функцияD может быть не определена.
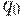 - начальное состояние.
- начальное состояние.
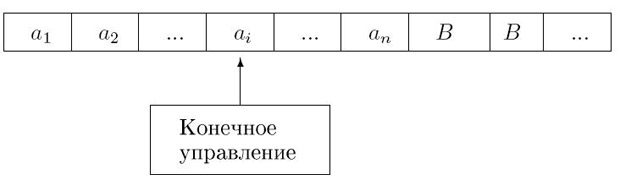
Рис. 2.2.Машина Тьюринга
Так определенная машина Тьюринга называется детерминированной. Недетерминированная машина Тьюринга для каждой пары 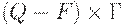 может иметь несколько возможных переходов. В начале n ячеек ленты содержат вход
может иметь несколько возможных переходов. В начале n ячеек ленты содержат вход 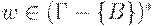 , остальная часть ленты содержит пустые символы. Обозначим конфигурацию машины Тьюринга как
, остальная часть ленты содержит пустые символы. Обозначим конфигурацию машины Тьюринга как 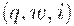 , где
, где 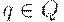 - текущее состояние, i - выделенный элемент строки, "положение головки" , w - текущее содержимое занятого участка ленты. Если головка сдвигается с ячейки, машина должна записать в нее символ, так что лента всегда состоит из участка, состоящего из конечного числа непустых символов и бесконечного количества пустых символов.
- текущее состояние, i - выделенный элемент строки, "положение головки" , w - текущее содержимое занятого участка ленты. Если головка сдвигается с ячейки, машина должна записать в нее символ, так что лента всегда состоит из участка, состоящего из конечного числа непустых символов и бесконечного количества пустых символов.
Шаг Tm определим следующим образом.
Пусть (q, A1, A2, ... An, i) - конфигурация Tm,
где 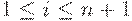 .
.
Если 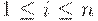 и D(q, Ai) = (p, A, R)
и D(q, Ai) = (p, A, R)
(R от англ. Right), то 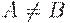 и)
и)
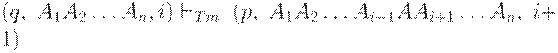
То есть Tm печатает символ A и передвигается вправо.
Если 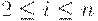 и
и 
( L от англ. Left), то если i = n, то допустимо A = B и
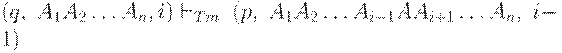
Tm печатает A и передвигается влево, но не за конец ленты.
Если i = n + 1, головка просматривает пустой символ B.
Если D(q, B) = (p, A, R), то 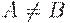 и
и
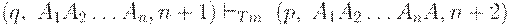
Если D(q, B) = (p, A, L), то допустимо A=B и
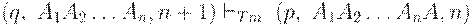
Если две конфигурации связаны отношением 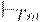 , то мы говорим, что вторая получается из первой за один шаг. Если вторая получается из первой за конечное, включая ноль, число шагов, то такое отношение будем обозначать
, то мы говорим, что вторая получается из первой за один шаг. Если вторая получается из первой за конечное, включая ноль, число шагов, то такое отношение будем обозначать  .
.
Язык, допускаемый Tm, это множество таких слов из T*, которые будучи расположены в левом конце ленты переводят Tm из начального состояния q0 с начальным положением головки в самом левом конце ленты в конечное состояние. Формально, язык, допускаемй Tm, это

Если Tm распознает L, то Tm останавливается, то есть не имеет переходов после того, как слово допущено. Однако, если словоне допущено, возможно, что Tm не останавливается.
Язык, допускаемый некоторой Tm, называется рекурсивно перечислимым. Если Tm останавливается на всех входах, то говорят, что Tm задает алгоритм и язык называется рекурсивным.
Существует машина Тьюринга, которая по некоторому описанию произвольной Tm и кодированию слова x моделирует поведениеTm со входом x. Такая машина Тьюринга называется универсальной машиной Тьюринга.
Дата добавления: 2016-06-13; просмотров: 1714;
