Представление языков

Процедура - это конечная последовательность инструкций, которые могут быть механически выполнены. Примером может служить машинная программа. Процедура, которая всегда заканчивается, называется алгоритмом.

Один из способов представления языка - дать алгоритм, определяющий, принадлежит ли цепочка языку. Более общий способ состоит в том, чтобы дать процедуру, которая останавливается с ответом "да" для цепочек, принадлежащих языку, и либо останавливается с ответом "нет", либо вообще не останавливается для цепочек, не принадлежащих языку. Говорят, что такая процедура или алгоритм распознает язык.

Такой метод представляет язык с точки зрения распознавания. Язык можно также представить методом порождения. А именно, можно дать процедуру, которая систематически порождает в определенном порядке цепочки языка.

Если мы можем распознать цепочки языка над алфавитом V либо с помощью процедуры, либо с помощью алгоритма, то мы можем и генерировать язык, поскольку мы можем систематически генерировать все цепочки из , проверять каждую цепочку на принадлежность языку и выдавать список только цепочек языка. Но если процедура не всегда заканчивается при проверке цепочки, мы не сдвинемся дальше первой цепочки, на которой процедура не заканчивается. Эту проблему можно обойти, организовав проверку таким образом, чтобы процедура никогда не продолжала проверять одну цепочку бесконечно. Для этого введем следующую конструкцию.

Предположим, что V имеет p символов. Мы можем рассматривать цепочки из как числа, представленные в базисе p, плюс пустая цепочка e. Можно занумеровать цепочки в порядке возрастания длины и в "числовом" порядке для цепочек одинаковой длины. Такая нумерация для цепочек языка 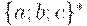приведена на рис. 2.1, а.

Пусть P - процедура для проверки принадлежности цепочки языку L. Предположим, что P может быть представлена дискретными шагами, так что имеет смысл говорить об i -ом шаге процедуры для любой данной цепочки. Прежде чем дать процедуру перечисления цепочек языка L, дадим процедуру нумерации пар положительных чисел.

Все упорядоченные пары положительных чисел (x, y) можно отобразить на множество положительных чисел следующей формулой:

z = (x + y - 1)(x + y - 2)/2 + y

Пары целых положительных чисел можно упорядочить в соответствии со значением z ( рис. 2.1, б).

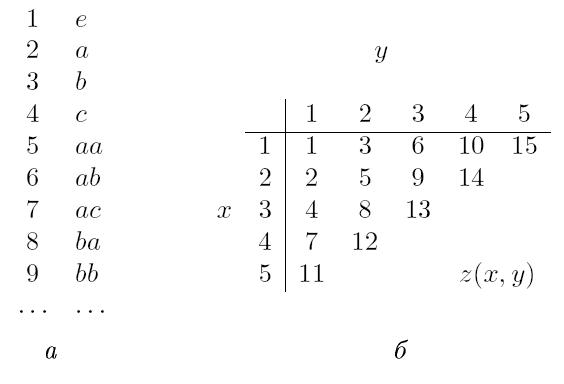
Рис. 2.1.

Теперь можно дать процедуру перечисления цепочек L. Нумеруем упорядоченные пары целых положительных чисел - (1,1), (2,1), (1,2), (3,1), (2,2), ... . При нумерации пары (i, j) генерируем i -ю цепочку из V* и применяем к цепочке первые j шагов процедуры P. Как только мы определили, что сгенерированная цепочка принадлежит L, добавляем цепочку к списку элементов L. Если цепочка i принадлежит L, это будет определено P за j шагов для некоторого конечного j. При перечислении (i; j) будет сгенерирована цепочка с номером i. Легко видеть, что эта процедура перечисляет все цепочки L.

Если мы имеем процедуру генерации цепочек языка, то мы всегда можем построить процедуру распознавания предложений языка, но не всегда алгоритм. Для определения того, принадлежит ли x языку L, просто нумеруем предложения L и сравниваем x с каждым предложением. Если сгенерировано x, процедура останавливается, распознав, что x принадлежит L. Конечно, если xне принадлежит L, процедура никогда не закончится.

Язык, предложения которого могут быть сгенерированы процедурой, называется рекурсивно перечислимым. Язык рекурсивно перечислим, если имеется процедура, распознающая предложения языка. Говорят, что язык рекурсивен, если существует алгоритмдля распознавания языка. Класс рекурсивных языков является собственным подмножеством класса рекурсивно перечислимых языков. Мало того, существуют языки, не являющиеся даже рекурсивно перечислимыми.

Грамматики