Соприкасающаяся плоскость кривой

Пусть PQ — касательная в точке Р к кривой γ (рис. 3). Через касательную PQ и точку M кривой проведем плоскость PQM. Плоскость π, к которой стремится плоскость PQM при М → Р, называется соприкасающейся плоскостью к кривой γ в точке Р.

Справедливо следующее утверждение.

Утверждение 2.1. Регулярная, дважды дифференцируемая кривая γ без особых точек имеет соприкасающуюся плоскость p каждой точке, в которой векторы 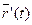и не коллинеарны.

Получим уравнение соприкасающейся плоскости в другой форме. Так как векторы 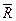– 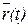, , 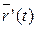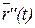компланарны, то вектор удовлетворяет следующему уравнению

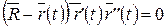Если X, У, Z — координаты вектора (координаты переменной точки s плоскости π), а х(t), у(t), z(t)— координаты вектора 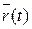, то в коор­динатной форме уравнение (2.1) запишется следующим образом:

Уравнение (2.2), очевидно, представляет собой уравнение соприка­сающейся плоскости.

Замечание 2.1. Соприкасающаяся плоскость определена гео­метрически с помощью предельного перехода, и поэтому в случае ее существования она будет единственна. Отсюда и из доказанного в этом пункте утверждения вытекает, что если в данной точке кривой существует соприкасающаяся плоскость, то при любой параметризации кривой вектор 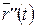параллелен этой плоскости.