Касательная прямая к кривой

Пусть задана гладкая кривая , и её уравнение имеет вид или

.

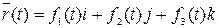Возьмём на линии две точки М и М₁, соответствующие значениям параметра t и 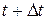(рис. 2). Вектор 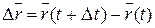является направляющим вектором секущей прямой ММ₁. Следовательно, вектор 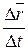также направляющий вектор секущей ММ₁. Когда , точка М₁ неограниченно приближается по кривой к точке М, вектор 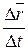стремится занять положение касательной в точке М (касательная к кривой в точке определяется как предельное положение секущей).

Вместе с тем отношение 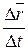стремится к производной 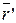как к своему пределу. Отсюда следует, что производная от радиус – вектора точки параметрической кривой есть вектор, направленный по касательной к этой кривой в сторону возрастания параметра t.

Чтобы получить уравнение касательной к вектор – функции, выразим радиус – вектор 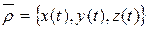любой точки касательной прямой через радиус – вектор 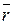начальной точки, направляющий вектор 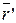и параметр .

Тогда – уравнение касательной в параметрическом виде.

Заменяя это векторное уравнение скалярными функциями, получим параметрические уравнения касательной:

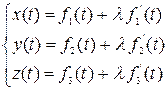
или, исключив параметр 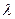, каноническое уравнение касательной:

.

Указанный способ определения касательной, очевидно, неприменим к той точке 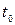, для которой . Такие точки будем называть особыми точками кривой и будем исключать их из рассмотрения.