Расчет наклонных сечений

Пример 34.Дано:колонна многоэтажного рамного каркаса с сечением размерами b = 400 мм, h = 600 мм; а = а' =50 мм; бетон класса В25 (R_b = 14,5 МПа, R_bt =1,05 МПа); хомуты, расположенные по граням колонны из арматуры класса А240 (R_sw= 170 МПа) диаметром 12 мм (А_sw= 226 мм²) шагом s_w = 400 мм; изгибающие моменты в верхнем и нижнем опорных сечениях равны М_sир = 350 кНм, M_inf = 250 кНм и растягивают соответственно левую и правую грани колонны; продольная сила N = 572 кН; длина колонны (расстояние между опорными сечениями) l = 3,3м .

Требуется проверить прочность колонны на действие поперечной силы .

Расчет. h_o= h - а =600 - 50 = 550 мм. Расчет производим согласно пп.3.30-3.32 с учетом рекомендаций п.3.52.

Поперечная сила в колонне равна

Поскольку поперечная сила постоянна по длине колонны, длину проекции наклонного сечения принимаем максимально возможной, т.е. равной c_max = 3h_o = 3·550 = 1650 мм < l = 2800 мм.

По формуле (3.84) определяем коэффициент φ_п2, принимая N_b =1,3R_bbh =13·14,5·400·600 = 4524·10³ Н = 4524 кН > N = 572 кН,

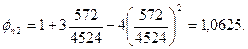
Поскольку с = c_max, Q_b = Q_b,min = 0,5R_btbh_o = 0,5·1,05·400·550 = 115500 H, а после умножения на φ_п2 Q_b = 111,5·1,0625 = 122,7 кН.

Значение q_sw определяем по формуле (3.48)

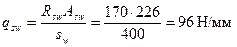
Определяем усилие в хомутах Q_sw, принимая c_o = 2h_o= 2·550 = 1100 мм, Q_sw = 0,75q_swс_о = 0,75·96·1100 = 79200 Н = 79,2 кН.

Проверяем условие (3.49), умножая его правую часть на φ_п2:

0,25R_btb·φ_п2 = 0,25·1,05·400·1,0625 = 111,6 Н/м > q_sw = 96 Н/мм. Поскольку условие (3.49) не выполняется, принимаем R_btb·φ_п2 = 4q_sw = 4·96 = 384 Н/мм, а следовательно,
Q_b = 0,5h_o R_btb·φ_п2 = 0,5·550·384 = 105600 Н= 105,6 кН

Проверяем условие (3.44):

Q_b + Q_sw= 105,6 + 79,2 = 184,8 > Q = 181,8 кН,

т.е. прочность наклонного сечения по поперечной силе обеспечена.