Прямоугольные сечения с симметричной арматурой
Пример 22. Дано:колонна среднего этажа рамного каркаса с сечением размерами b = 400 мм, h = 500 мм; а = а' = 40 мм; бетон класса В25 (Еb = 300000 МПа, Rb = 14,5 МПа); арматура класса А400 (Rs = Rsc = 355 МПа); площадь ее сечения Аs = А's= 1232 мм2 (2Æ28); продольная сила и изгибающие моменты в опорном сечении: от вертикальных нагрузок: всех Nv = 650 кН, Mv = 140 кН м, постоянных и длительных Nl = 620 кН, Мl = 130 кНм.; от ветровых нагрузок Nh = 50 кН, Mh = 73 кН м; высота этажа l = 6 м.
Требуется проверить прочность опорного сечения колонны.
Расчет. hо = 500 - 40 = 460 мм. Расчет ведем с учетом влияния прогиба согласно п.3.53. Поскольку рассматриваемое сечение опорное и колонна у этой опоры имеет податливую заделку, принимаем ηv = 1,0. Для вычисления коэффициента ηh принимаем согласно п.3.55,б расчетную длину колонны равной lo = 1,2·6 = 7,2 м. При этом lo/h =7,2/0,5 = 14,4 > 4, т.е. учет прогиба обязателен.
Усилия от всех нагрузок равны М = Mv + Mh = 140 + 73 = 213 кН·м, N = Nv + Nh= 650 + 50 = 700 кН. При этом, 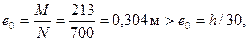 т.е. согласно п.3.49 значение момента М не корректируем.
т.е. согласно п.3.49 значение момента М не корректируем.
Определяем моменты М1и М1l относительно растянутой арматуры соответственно от всех нагрузок и от постоянных и длительных нагрузок
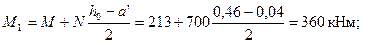
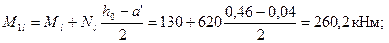
Тогда φl = 1 +М1l/М1= 1 + 260,2/360 = 1,72.
Так как 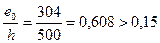 , принимаем δe = 0,608.
, принимаем δe = 0,608.
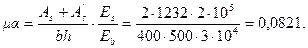
По формуле (3.89) определим жесткость D
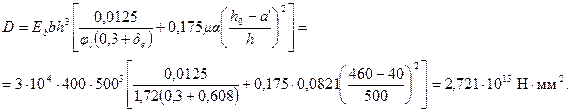
Отсюда 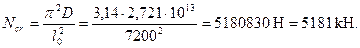
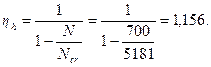
Расчетный момент с учетом прогиба определяем по формуле(3.85), принимая Мt = 0,0.
М = Mvηv + Mhηh = 140 + 73·1,156 = 224,4 кНм.
Проверяем прочность сечения согласно п.3.56.
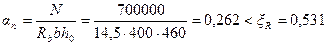 (см. табл. 3.2).
(см. табл. 3.2).
Следовательно, х = anhо = 0,262·460 = 120,5 мм.
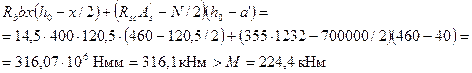
т.е. прочность сечения обеспечена.
Пример 23.Дано:сечение колонны среднего этажа рамного каркаса размером b = 400 мм, h = 400 мм; а = а' = 50 мм; бетон класса В25 (Rb = 14,5 МПа, Еb = 3·105 МПа); арматура симметричная класса А400 (Rs = Rsc = 355 МПа); продольная сила и изгибающие моменты в опорном сечении: от вертикальных нагрузок: всех Nv = 900 кН, Mv = 160 кНм; постоянных и длительных Nl = 800 кН, Ml = 150 кНм; от ветровых нагрузок Nh = 100 кНм, Mh = 110 кНм; высота этажа 4,8 м.
Требуется определить площадь сечения арматуры.
Расчет. ho = 400 - 50 = 350 мм. В соответствии с п.3.53 принимаем ηv = 1,0, а согласно п.3.55,б расчетную длину колонны принимаем равной lo = 1,2·4,8 = 5,76 м.
При этом l0/h = 5,76/0,4 = 14,4 > 4, т.е. учитываем прогиб колонны.
Усилия от всех нагрузок равны М = Mv + Mh = 160 + 110 = 270 кНм; N =Nv + Nh = 900 + 100 = 1000 кН. При этом 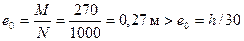 , т.е. значение М не корректируем.
, т.е. значение М не корректируем.
Согласно п.3.54 определяем коэффициент ηh.
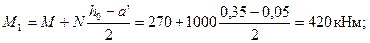
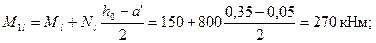
φl = 1 +М1l/М1= 1 + 270 /420 = 1,64.
Так как 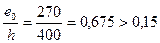 , принимаем δe = 0,675.
, принимаем δe = 0,675.
В первом приближении принимаем μ = 0,01,
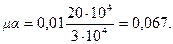
По формуле (3.89) определяем жесткость D:
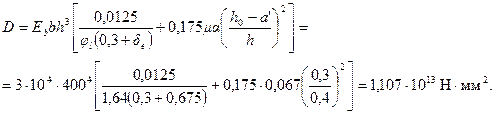
Отсюда 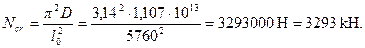
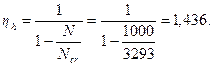
М = Mvηv + Mhηh = 160·1,0 + 110·1,436 = 318 кН·м.
Необходимую площадь сечения арматуры определим согласно п.3.57. Для этого вычислим значения:
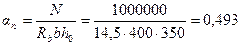
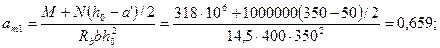
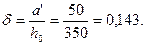
Из табл. 3.2 находим ξR = 0,531. Так как аn < ξR, Аs = А's определим по формуле (3.93)
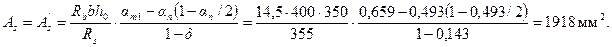
Откуда 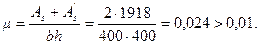
Поскольку полученное армирование превышает армирование, принятое при определении D, а момент Мh = 110 кНм составляет значительную долю полного момента М = 270 кНм, значение As = 1918 мм2 определено с некоторым «запасом», который можно уменьшить, повторив расчет, принимая в формуле (3.89) значение μ = 0,024:
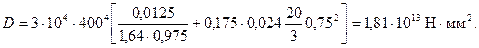
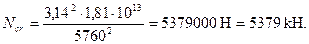
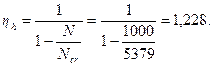
М =160·1,0 + 110·1,228 = 295 кН·м.
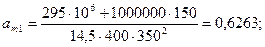
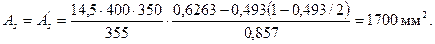
Принимаем значения Аs = А's =1847 мм2 (3Æ28), что близко к значению Аs использованному при вычислении D.
Пример 24.Дано:колонна нижнего этажа многоэтажного рамного каркаса с сечением размерами b = 400 мм, h = 500 мм; а = а' = 50 мм; бетон класса В25 (Еb = 3·104 МПа, Rb = 14,5 МПа); арматура класса А400 (Rs = Rsc = 355 МПа) с площадью сечения As = А's = 1847 мм2 (3Æ28); продольные силы и изгибающие моменты в нижнем опорном сечении: от вертикальных нагрузок: всех Nv = 2200 кН, Mv = 250 кНм, от постоянных и длительных нагрузок Nl = 2100 кН, Ml = 230 кНм; от ветровых нагрузок Nh = 0,0, Mh = 53 кНм; высота этажа 6 м.
Требуется проверить прочность нижнего опорного сечения колонны.
Расчет. ho = h - а = 500 - 50 = 450 мм. Расчет ведем с учетом прогиба колонны согласно п.3.53. Поскольку у рассматриваемого сечения колонна жестко заделана в фундамент, коэффициент ηv определяем по формуле (3.86), принимая расчетную длину колонны согласно п. 3.55 а равной lo = 0,7·6 = 4,2 м.
Жесткость D при определении как коэффициента ηv так и коэффициента ηh вычисляем по формуле (3.89) с учетом всех нагрузок. Усилия от всех нагрузок равны М = Mv + Мh = 250 + 53 = 303 кН, N = Nv = 2200 кН. При этом 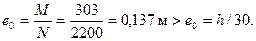
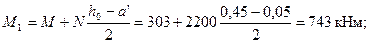
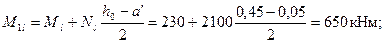
φl = 1 +М1l/М1= 1 + 650 /743 = 1,875.
Так как 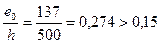 , принимаем
, принимаем 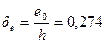 .
.
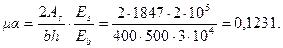
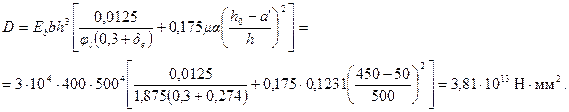
Отсюда 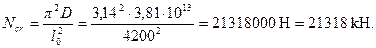
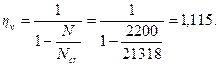
Аналогично определим коэффициент ηh принимая расчетную длинусогласно п.3.55,б равной lo = 1,0·6 = 6 м. Тогда
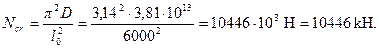
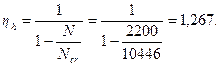
Расчетный момент с учетом прогиба равен
М = Mvηv + Mhηh = 250·1,115 + 53·1,267 = 345,9 кНм.
Проверяем прочность сечения согласно п.3.56.
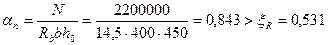 (см. табл. 3.2).
(см. табл. 3.2).
Следовательно, высоту сжатой зону х определяем с помощьюформулы (3.92). Для этого вычисляем
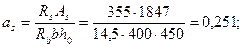
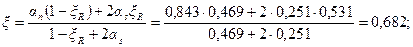
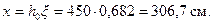
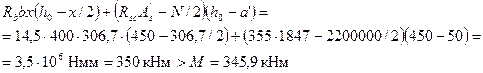
т.е. прочность сечения обеспечена.
Пример 25. Дано:колонна нижнего этажа связевого каркаса с сечением размерами 400x400 мм; а = а' = 50 им; бетон класса В40 (Еb= 36·103 МПа, Rb = 22 МПа); продольная арматура класса А500 (Rs = 435 МПа, Rsc = 400 МПа); продольные силы и изгибающие моменты в нижнем опорном сечении от вертикальных нагрузок Nv = 6000 кН, Мv = 120 кНм, от постоянных и длительных нагрузок Nl = 5800 кН, Ml = 100 кНм; усилиями от ветровой нагрузки пренебрегаем; высота этажа l = 3,6 м.
Требуется определить площадь сечения продольной арматуры.
Расчет. hо = 400 - 50 = 350 мм. Расчет ведем с учетом прогиба колонны согласно п.3.53. Поскольку у рассматриваемого сечения колонна жестко заделана в фундамент, коэффициент ηv определяем по формуле (3.85), принимая расчетную длину колонны согласно п.3.55,а, равной lo = 0,7·3,6 = 2,52 м.
При этом lo/h = 2,52/0,4 = 6,3 > 4, т.е. учет прогиба обязателен. Определяем по формуле (3.89) жесткость D,учитывая все нагрузки, т.е. М = Мv = 120 кНм и N = Nv = 6000 кН. Эксцентриситет 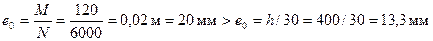 , следовательно, момент не корректируем.
, следовательно, момент не корректируем.
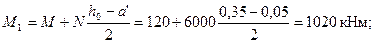
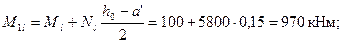
φl = 1 +М1l/М1= 1 + 970 /1020 = 1,951.
Так как 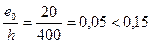 , принимаем
, принимаем 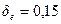 .
.
В первом приближении принимаем μ = 0,02, тогда 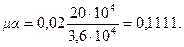
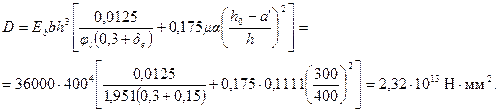
Отсюда 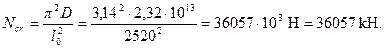
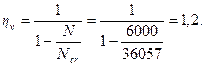
М = Mvηv = 120·1,2 = 144 кНм.
Необходимую площадь сечения арматуры определим согласно п.3.57.Для этого вычислим значения:
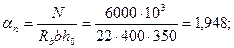
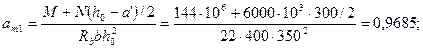
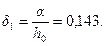
Из табл. 3.2 находим ξR = 0,493. Так как an > ξR, значение As= А's определяем по формуле (3.94). При этом, поскольку здесь определяющим прочность является сжатая арматура, принимаем Rs = Rsc = 400 МПа. Значение ξ определяем по формуле (3.92), вычисляя as по формуле (3.95) при
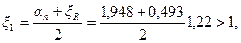 т.е. при ξ1 = 1,0
т.е. при ξ1 = 1,0
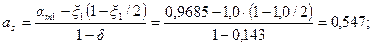
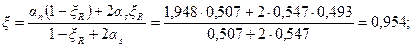
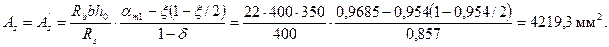
Принимаем Аs = А's = 4539 мм2 (2Æ40 + 2Æ36).
Пример 26.Дано:колонна среднего этажа связевого каркаса с сечением размерами 400x400 мм; бетон класса В25 (Rb = 14,5 МПа), продольная арматура класса А400 (Rs = Rsc = 355 МПа): продольные силы и изгибающие моменты от вертикальных нагрузок в опорном сечении: от всех нагрузок Nv = 2200 кН, Mv =20 кН м, от постоянных и длительных нагрузок Nl = 1980 кН, Мl = 0,0; высота этажа Н = 6 м.
Требуется определить площадь сечения продольной арматуры.
Расчет. Поскольку колонна закреплена с обоих концов шарнирно опертыми ригелями, принимаем согласно п.3.59,арасчетную длину колонны равной lo = Н = 6 м. Тогда lo/h = 6/0,4 = 15 > 4, т.е. учет прогиба колонны обязателен.
Эксцентриситет продольной силы от всех нагрузок равен 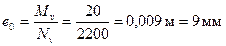 . Поскольку
. Поскольку 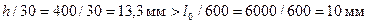 , согласно п.3.49 случайный эксцентриситет принимаем равным еа= 13,3 мм > еo. Следовательно, расчет колонны производим на действие продольной силы с эксцентриситетом еo = еа согласно п.3.58.
, согласно п.3.49 случайный эксцентриситет принимаем равным еа= 13,3 мм > еo. Следовательно, расчет колонны производим на действие продольной силы с эксцентриситетом еo = еа согласно п.3.58.
Из табл.3.5 и 3.6 при Nl/N = 1980/2200 = 0,9, предполагая отсутствие промежуточных стержней при а = а' < 0,15 h находим φb = 0,804 и φsb = 0,867.
Принимая в первом приближении φ = φsb = 0,867, из условия (3.97) находим
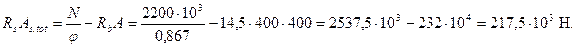
Отсюда 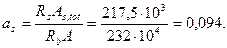
Поскольку аs < 0,5, уточняем значение φ, вычислив его по формуле (3.98):
φ = φb + 2(φsb - φb)as = 0,804 + 2(0,867 - 0,804)0,094 = 0,816.
Аналогично определяем
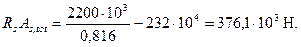
Полученное значение RsAs,tot существенно превышает принятое в первом приближении, поэтому еще раз уточняем значение φ :
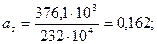
φ = 0,804 + 2(0,867-0,804)0,162 = 0,824;
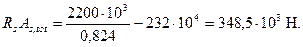
Поскольку полученное значение RsAs,tot близко к принятому во втором приближении, суммарную площадь сечения арматуры принимаем равной
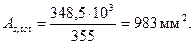
Окончательно принимаем As,tot = 1018 мм2 (4Æ18).
Дата добавления: 2016-05-25; просмотров: 769;
