Двутавровые сечения

Пример 28. Дано:колонна одноэтажного промздания: размеры сечения и расположение арматуры - по черт.3.34; бетон класса В30 (Е_b = 32500 МПа, R_b = 17,0 МПа); арматура класса А400 (R_s = R_sc = 355 МПа), площадь сечения A_s = A^'_s =5630 мм² (7Æ32); продольные силы и изгибающие моменты в нижнем опорном сечении: от вертикальных нагрузок: всех N_v = 6000 кН, M_v = 1000 кНм, от постоянных и длительных нагрузок N_l = 5000 кН, M_l = 750 кНм; от ветровых нагрузок N_h = 0,0, М_h = 2000 кНм; высота колонны Н = 15 м.

Требуется проверить прочность сечения.

Черт.3.34. К примерам расчета 28 и 29

Расчет в плоскости изгиба. Расчет ведем с учетом прогиба колонны согласно п.3.53. Поскольку у рассматриваемого сечения колонна жестко заделана в фундамент, коэффициент η_v определяем по формуле (3.86), принимая расчетную длину колонны согласно п.3.55,а равной l_o = 0,7H = 0,7·15=10,5 м.

Определим жесткость D по формуле (3.88), учитывая все нагрузки.

Принимаем расчетную толщину полки равной средней высоте свесов h'_f = h_f= 200 + 30/2 = 215 мм.

Вычислим площадь и момент инерции бетонного сечения:

А = 200·1500 + 2·400·215 = 472·10³ мм²;

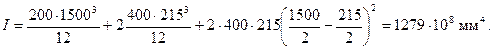
Радиус инерции сечения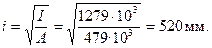

Так как l_o/i = 10500/520 = 20,2 > 14, учет прогиба колонныобязателен.

Усилия от всех нагрузок:

М = M_v + M_h= 1000 + 2000 = 3000 кНм;

N = N_v = 6000 кН;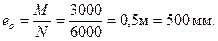

Определим момент инерции сечения всей арматуры. Центр тяжести арматуры A_s и A^'_s отстоит от ближайшей грани на расстоянии 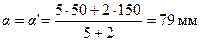, откуда h_о = h - а = 1500 – 79 = 1421 мм.

0,5h - а = 750 - 79 = 671 мм.

I_s = 2 A_s (0,5h - а)²= 2·5630·671² = 5,07·10⁹ мм⁴.

Определим коэффициент φ_l:

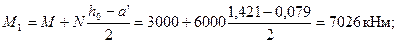
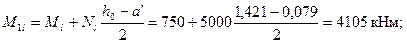
φ_l = 1 +М_1l/М₁= 1 + 4105 /7026 = 1,584.

Так как 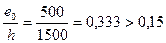, принимаем .

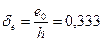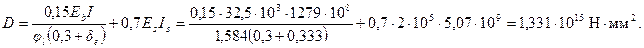
Отсюда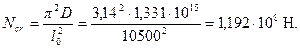

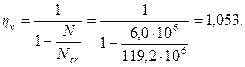
Аналогично определим коэффициент η_h принимая расчетную длинусогласно п.3.55,б равной l_o = 1,5H = 1,5·15 = 22,5 м:

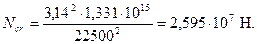
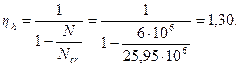
Расчетный момент с учетом прогиба равен

М = M_vη_v + M_hη_h = 1000·1,05 + 2000·1,3 = 3653 кНм.

Проверим условие (3.108):

R_bb^'_fh^'_f = 17·600·215 = 2193·10³ Н = 2193 кН < N = 6000 кН,

т.е. расчет производим как для двутаврового сечения.

Площадь сжатых свесов полки равна:

А_ov. = (b^'_f - b)h^'_f = (600 - 200)215 = 86000 мм².

Определим высоту сжатой зоны х.

Так как 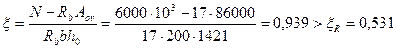(см. табл. 3.2), значение х определяем по формуле (3.110).

Для этого вычисляем

R_bbh₀ = 17·200·1421 = 4831400 Н;

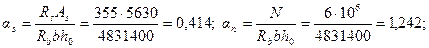
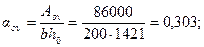
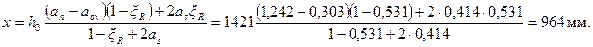
Прочность проверяем из условия (3.109):

R_bbx(h_o - x/2)+R_bA_ov(h_o - h'_f/2)+(R_scA'_s - N/2)(h_o - a') = 17·200·964·(1421 - 964/2) +

+ 17·86000· (1421 - 215/2)+(355·5630 - 6·10⁶/2) · (1421 - 79) = 3,654·10⁹ Н·мм =

= 3654 кН·м >М= 3653 кН·м,

т.е. прочность сечения в плоскости изгиба обеспечена.

Расчет из плоскости изгиба. Определим радиус инерции сечения из плоскости изгиба:

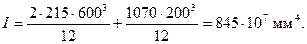
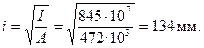
Так как гибкость из плоскости изгиба l_o/i = 10500/134 =78,4 заметно превышает гибкость в плоскости изгиба l_o/i = 20,2, согласно п.3.50 следует проверить прочность сечения из плоскости изгиба, принимая эксцентриситет е_о, равным случайному эксцентриситету е_а. Высота сечения при этом равна h = 600 мм. Определяем значение е_а согласно п.3.49.

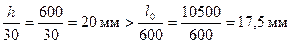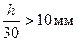Поскольку , и , принимаем 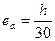, что при 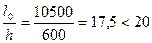позволяет производить расчет согласно п.3.58; при этом коэффициент φ определяем как для прямоугольного сечения, не учитывая "в запас" сечение ребра, т.е. при b = 2·215 = 430 мм.

Поскольку число промежуточных стержней Æ32, расположенных вдоль обеих полок, равное 6 превышает 1/3 числа всех стержней Æ32 14/3 = 4,67, в расчете используем табл.3.6 (разд. Б). Из этой таблицы приN_l/N= 5000/6000= 0,833 иl_o /h =17,5 находим φ_sb = 0,736.

А_s,tot = 11260 мм² (14Æ32). Значение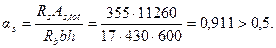

Следовательно, φ = φ_sb = 0,736.

Проверим условие (3.97):

φ(R_bA + R_scA_s,_tot) = 0,736(17·472·10³ + 355·11260) = 8848·10³ H >N = 6000 кН,

т.е. прочность из плоскости изгиба обеспечена.

Пример 29.Дано:колонна с податливыми заделками по обеим концам; сечение и расположение арматуры - по черт.3.34; бетон класса В30 (R_b = 17,0 МПа); арматура симметричная класса А400 (R_s = R_sc = 355 МПа); продольная сила и момент в опорном сечении от вертикальных нагрузок N = 6000 кН, М = 3000 кНм, усилия от ветровых нагрузок отсутствуют (M_h = 0,0, N_h = 0).

Требуется определить площадь сечения арматуры для опорного сечения колонн.

Расчет в плоскости изгиба. Согласно п.3.53 коэффициент η_v =1,0, а поскольку M_h = 0, коэффициент η_h не вычисляем. Следовательно, прогиб элемента в плоскости изгиба не учитываем.

Из примера 28 имеем: h^'_f = 215мм, h_о = 1421 мм, а' = 79 мм.

Проверим условие (3.108):

R_bb^'_f h^'_f = 17·600·215 = 2193·10³ Н = 2193 кН < N= 6000 кН,

т.е. расчет производим как для двутаврового сечения согласно п.3.61.

Площадь сжатых свесов полки равна:

A_ov=(b^'_f - b)h^'_f = (600 - 200)·215 = 86000 мм².

Определяем значения а_n , а_m1, а_ov , а_m,ov ,δ.

R_bbh_o = 17·200·1421 = 4831400 Н.

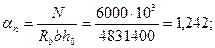
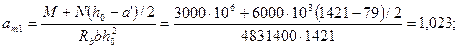
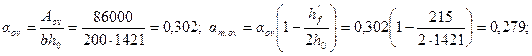
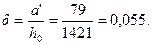
Из табл. 3.2 находим ξ_R = 0,531.

Так как ξ = а_n - а_ov = 1,242 - 0,302 = 0,94 > ξ_R = 0,531, площадь сечения арматуры определяем по формуле (3.113). Для этого по формулам (3.114) и (3.110) вычисляем значения а_s и ξ₁= x/h_o.

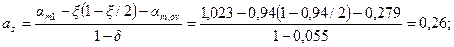
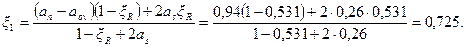
Отсюда

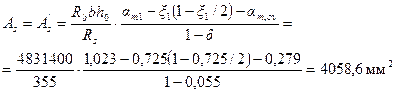
Принимаем A_s = A'_s = 4310 мм² (7Æ28). Расчет из плоскости изгиба производим аналогично примеру 28.

Кольцевые сечения

Пример 30.Дано:консольная стойка высотой Н = 6 м, сечение с внутренним радиусом r₁= 150 мм, наружным – r₂ = 250 мм; бетон класса В25 (Е_b = 3·10⁴ МПа, R_b= 14,5 МПа); продольная арматура класса А400 (R_s = R_sc = 355 МПа) располагается посредине толщины кольца, площадь ее сечения A_s,tot = 1470 мм² (13Æ12); продольная сила и момент в заделке: от вертикальных нагрузок: N_v = 120 кН, M_v =40 кН.м; от ветровых нагрузок: N_h = 0, M_h = 70 кН.м.

Требуется проверить прочность сечения

Расчет. Внутренний и наружный диаметры равны D₁ = 2r₁ = 300мм, D₂ = D_{ci r}= 2r₂ = 500 мм.Поскольку для консольной стойки эксцентрично приложенная вертикальная сила вызывает смещение верха, в соответствии с п.3.53 принимаем M_l = 0 и M_h = 40 + 70 = 110 кНм. Коэффициент η_h определяем по формуле (3.85), принимая согласно п.3.55,б расчетную длину стойки равной l_o = 2H =3·6=12 м. Усилия от всех нагрузок равны:

N = 120 кН, М = M_h = 110 кНм

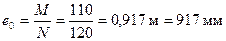
Определяем жесткость D по формуле (3.88);

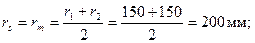
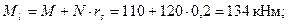
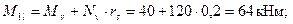
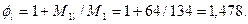
Поскольку 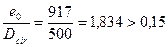, принимаем .

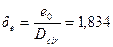Моменты инерции бетонного сечения и всей арматуры соответственно равны

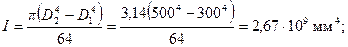
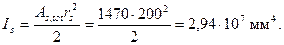
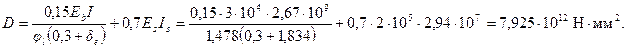
Отсюда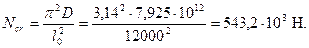

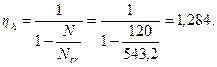
Момент с учетом прогиба равен М = 110·1,284 = 141,2 кНм,

Площадь сечения равна

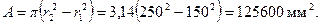
Вычисляем относительную площадь сжатой зоны бетона по формуле (3.115):

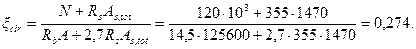
Так как 0,15 < ξ_cir < 0,6, прочность сечения проверяем из условия (3.116):

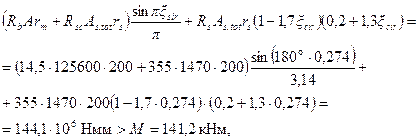
т.е. прочность сечения обеспечена.

Круглые сечения

Пример 31. Данo:колонна нижнего этажа рамного каркаса длиной 4,8м; сечение диаметром D_cir = 400 мм; а = 35 мм; бетон класса В25 (Е_b = 3·10⁴ МПа, R_b = 14,5 МПа); продольная арматура класса А400 (R_s = R_sc = 355 МПа); площадь ее сечения A_s,tot = 3140 мм² (10Æ20); продольные силы и моменты в верхнем опорном сечении: от вертикальных нагрузок N_v = 1700 кН; M_v = 60 кНм; от ветровых нагрузок N_h = 100 кН, M_h = 45 кНм, кратковременные вертикальные нагрузки отсутствуют.

Требуется проверить прочность верхнего опорного сечения.

Расчет. Поскольку рассматриваемое сечение расположено у податливой заделки, согласно п.3.53 η_v = 1,0. Определяем коэффициент η_h согласно п.3.54. При этом расчетную длину принимаем согласно п.3.55,б равной l_o = H = 4,8 м. Усилия от всех нагрузок равны:

М = M_v + M_h = 60 + 45 = 105 кНм, N = N_v + N_h = 1700 + 100 = 1800 кН;

.

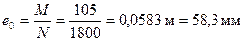Определяем жесткость D по формуле (3.88). Для этого вычисляем: r = D_cir /2= 400/2= 200 мм, r_s = r - а = 200 - 35 = 165 мм;

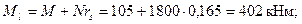
В связи с отсутствием вертикальных кратковременных нагрузок M_l = M_v = 80 кНм

N = N_v = 1700 кН; тогда

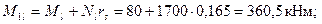
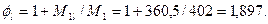
Так как 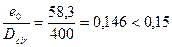, принимаем .

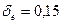Момент инерции бетонного сечения и всей арматуры соответственно равны:

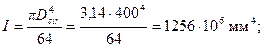
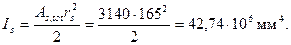
Тогда

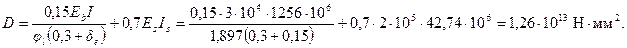
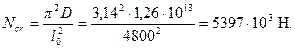
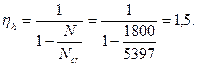
Расчетный момент с учетом прогиба равен

M = M_v + M_h η_h = 60 + 45·1,5 = 127,5 кНм

Прочность сечения проверяем из условия (3.127) с помощью графикана черт.3.33. Определим площадь бетонного сечения

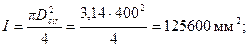
По значениям ,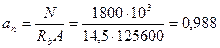

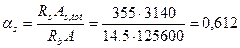
и

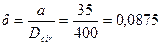на графике находим а_т = 0,375.

а_тR_bАr= 0375·14,5·125600·200 = 136,6·10⁶ Нмм > М = 127,5 кНм,

т.е. прочность сечения обеспечена.