Параллельное соединение элементов R, L, C

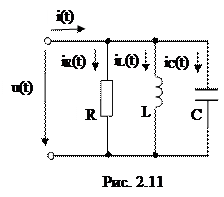
На вход электрической цепи (рис. 2.11), состоящей из соединенных параллельно элементов R, L, C подано синусоидальное напряжение

u(t) = U_msin(ωt+ψ_u).

Запишем уравнение по первому закону Кирхгофа для мгновенных значений токов цепи:

.

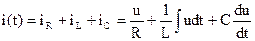Сумме синусоидальных токов соответствует сумма изображающих их комплексных величин. Тогда для действующих комплексных значений можно записать:

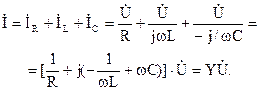
Величину называют комплексной проводимостью цепи с параллельным соединением элементов R, L, C, которая определяется как сумма проводимостей параллельных ветвей;

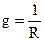– активная составляющая проводимости;

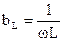– реактивная индуктивная составляющая проводимости;

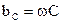– реактивная емкостная составляющая проводимости.

Необходимо заметить, что в том случае если ветвь содержит не один, а несколько элементов, то активная и реактивная составляющие полной проводимости такой ветви будут определяться:

, .

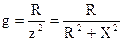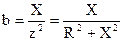Запишем комплексную проводимость в показательной форме:

.

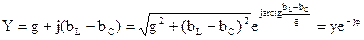Тогда комплексный ток можно записать как:

,

где 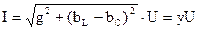– действующее значение входного тока;

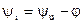– начальная фаза тока;

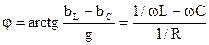– угол сдвига фаз между напряжением на зажимах цепи и входным током, который определяется соотношением активной и реактивной проводимостей.

Построим векторную диаграмму токов и напряжения на зажимах цепи (рис. 2.12), приняв начальную фазу напряжения за ноль.

Ток активного элемента совпадает по фазе с напряжением, поэтому на векторной диаграмме вектор этого тока изображается параллельно вектору напряжения. Ток индуктивного элемента отстает от напряжения на 90 градусов, поэтому на векторной диаграмме индуктивный ток повернут относительно вектора напряжения на 90 градусов по направлению движения часовой стрелки. Ток емкостного элемента опережает напряжение на 90 градусов, поэтому емкостный ток повернут относительно вектора напряжения против направления часовой стрелки на 90 градусов.

Необходимо отметить, что ток индуктивного и емкостного элементов находятся в противофазе, вследствие чего в цепи переменного тока при параллельном соединении этих элементов могут создаваться условия, невозможные для цепей постоянного тока, когда токи отдельных элементов будут значительно превышать входной ток.

Треугольник, образованный векторами токов, принято называть треугольником токов.

Если каждую сторону треугольника токов поделить на вектор напряжения, то получим треугольник (рис. 2.13), подобный исходному и называемый треугольником проводимостей.

Как видно из полученных векторных диаграмм (рис. 2.12 и 2.13), угол сдвига фаз зависит от соотношения параметров цепи:

при угол φ > 0, ток отстает по фазе от напряжения;

при 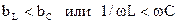угол φ < 0, ток опережает по фазе напряжение;

при 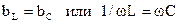угол φ = 0, ток совпадает по фазе с напряжением и цепь ведет себя как чисто активное сопротивление; такой режим работы цепи называется режимом резонанса токов.