Последовательное соединение элементов R, L, C

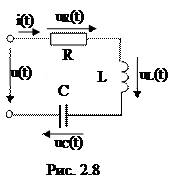
Пусть в цепи, состоящей из последовательно соединенных элементов R, L, C (рис. 2.8), известен ток i(t) = I_msin(ωt + ψ_i) и необходимо определить напряжение на ее зажимах.

Запишем для цепи уравнение по второму закону Кирхгофа для мгновенных значений напряжений:

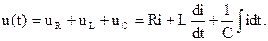
Сумме синусоидальных напряжений соответствует сумма изображающих их комплексных величин. Тогда для действующих комплексных значений можно записать:

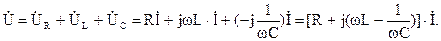Комплексное действующее значение напряжения:

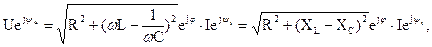
где 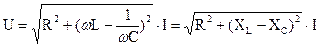– действую-щее значение напряжения, приложенного к цепи;

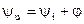– начальная фаза напряжения;

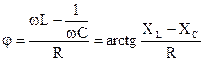– угол сдвига фаз между напряжением на зажимах участка цепи и током; сдвиг фаз определяется соотношением реактивных и активных сопро-тивлений, включенных на этом участке.

Так как амплитудные значения тока и напряжения связаны с действующими значениями соотношениями:

, ,

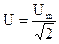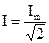то амплитудное значение входного напряжения запишется:

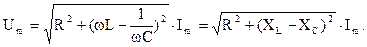
Запишем мгновенное значение напряжения на входе цепи, которое при синусоидальном токе также будет изменяться по синусоидальному закону:

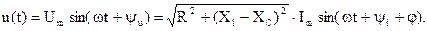
Введем еще ряд величин, характеризующих цепь синусоидального тока.

Величину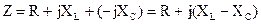

называют комплексным сопротивлением цепи с последовательным соединением элементов R, L, C. Заметим, что в этом случае комплексные сопротивления отдельных участков цепи складываются, как и сопротивления цепи постоянного тока.

Запишем комплексное сопротивление в показательной форме:

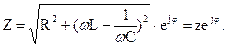
Модуль комплексного сопротвления:

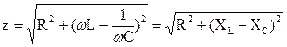– называют полным сопротивлением цепи.

Аргумент комплексного сопротивления:

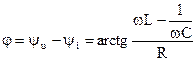– угол сдвига фаз между входным напряжением и током.

При 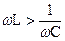угол φ>0, ток отстает по фазе от напряжения. При 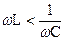угол φ <0, ток опережает напряжение по фазе. При 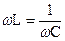угол φ=0, ток совпадает по фазе с напряжением и цепь ведет себя, как чисто активное сопротивление. Такой режим работы цепи называют резонансным режимом.