Понятие линейной однофакторной регрессии

Одна из наиболее простых эконометрических моделей – простая (парная) линейная регрессия. Парная регрессия используется в том случае, когда из всего круга факторов, влияющих на результат, можно выделить один, оказывающий сильное влияние. Он и используется в качестве объясняющей переменной. Представим, что у нас есть два ряда данных:

;

;

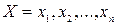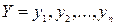где 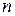– число наблюдений. Каждое из наблюдений характеризуется двумя переменными 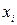и .

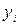Линейная однофакторная регрессия – уравнение связи результативного показателя и фактора в виде линейного уравнения:

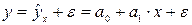или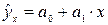

где 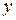– зависимая (объясняемая) переменная, реальная или фактическая или, как её ещё называют, эмпирическая, то есть, наблюдавшаяся в действительности;

x – независимая (объясняющая) переменная;

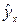– зависимая переменная (результат), рассчитанная с помощью уравнения регрессии, ещё её называют теоретической (в данном случае она рассчитывается по линейному уравнению регресси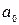и);

и 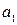– константы, параметры уравнения линейной регрессии;

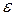– случайная компонента, или возмущение.

Случайная компонента 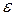по своей сути есть случайная величина, характеризующая влияние не учтенных в модели факторов, каких-либо случайных влияний, неправильный выбор специфики модели и, в некоторых случаях, может быть связана с особенностями измерения.

Каждую пару наблюдений ( 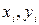) можно отобразить в качестве точки на плоскости 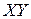. Такое графическое построение называется полем корреляции.

Рис. 1. – Линия регрессии

В каждом из наблюдений величину случайной компоненты можно определить как разность между фактическим значением результата и рассчитанным по уравнению регрессии:

.

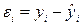Если на графике все точки ( 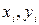) совпадают с линией регрессии, тогда между результативным признаком 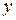и фактором 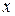существует строгая функциональная связь и выполняется следующее равенство:

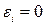для каждого .

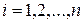В экономических процессах такое практически не встречается, но во всех случаях, когда применение МНК оправдано, верно, что 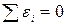, поэтому в качестве меры отклонений используется сумма квадратов отклонений 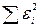, в частности используется остаточная дисперсия.

2. Определение параметров линейной регрессии

методом наименьших квадратов (МНК)

Для нахождения параметров 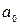и 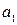уравнения линейной регрессии обычно используется метод наименьших квадратов – метод определения зависимости результирующего показателя от факторов путем минимизации суммы квадратов отклонений фактических значений результирующего показателя от значений, определяемых уравнением регрессии.

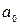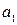Сущность метода наименьших квадратов заключается в нахождении параметров модели и , при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:

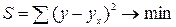. (1)

Для линейной однофакторной модели:

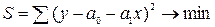. (2)

Функция двух переменных 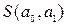может достигнуть экстремума в том случае, когда первые частные производные этой функции равняются нулю, т.е. когда

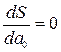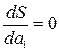и (3)

Вычисляя эти частные производные, получим:

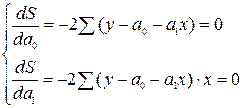(4)

После несложных преобразований получаем систему нормальных уравнений для определения величины параметров 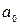и 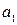, уравнения линейной однофакторной модели:

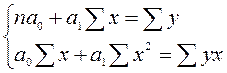(5)

где 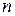– объем исследуемой совокупности (число единиц наблюдений).

В уравнении регрессии свободный член регрессии коэффициент 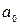показывает совокупное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; его вклад в значение результирующего показателя не зависит от изменения факторов.

Параметр 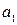– коэффициент регрессии – показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения. При наличии прямой связи 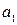имеет положительное значение, и при увеличении фактора результат увеличивается и линия регрессии возрастающая. В случае обратной связи коэффициент регрессии отрицательный, и при возрастании фактора результат уменьшается, в этом случае линия регрессии имеет отрицательный наклон.

Для определения величин 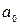и 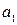необходимо вычислить следующие значения: 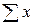, , 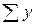, 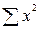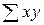. Расчеты рекомендуется проводить в таблице:

Таблица 1 – расчет параметров уравнения регрессии

N п/п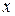
….
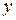
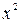
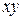
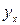
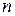
Итого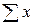

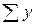
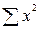
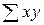
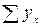
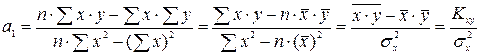(6)

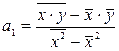(7)

Параметр 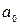оценивается по следующей формуле:

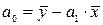. (8)

Правильность расчета параметров уравнения регрессии может быть проверена с помощью сравнения сумм 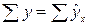. На практике из-за округления при расчетах возможно некоторое расхождение.

Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:

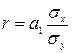(9)

Коэффициент регрессии применяют для определения коэффициента эластичности, который показывает, на сколько процентов изменится величина результативного признака 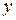при изменении факторного 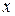на один процент.

Для определения коэффициента эластичности используется формула:

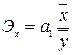(10)

где 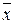, 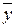– средние значения признаков, вычисляемых:

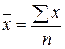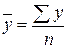, (11)

3. Оценка существенности уравнения линейной регрессии

После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Оценка значимости уравнения регрессии в целом осуществляется с помощью критерия Фишера, так называемого 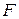-критерия. При этом выдвигается нулевая гипотеза 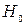, что коэффициент регрессии равен нулю, то есть 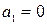, а значит фактор 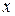не оказывает влияния на результат 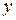и линия регрессии параллельна оси абсцисс.

Для определения 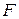-критерия необходимо рассчитать дисперсии на одну степень свободы .

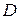Общую сумму квадратов отклонений 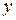от 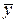можно разложить на суммы – объясненную регрессией и необъясненную:

,

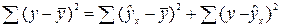где 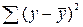– общая сумма квадратов отклонений индивидуальных значений результата от среднего по выборке;

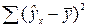– сумма квадратов отклонений, объясненная регрессией;

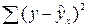– сумма квадратов отклонений, необъясненная регрессией, ещё её называют остаточной суммой квадратов отклонений.

Любая сумма квадратов отклонений связана с числом степеней свободы 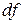, то есть с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности 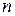и с числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должно показать, сколько независимых отклонений из 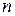возможных 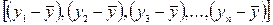требуется для образования данной суммы квадратов. Для общей суммы квадратов 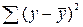требуется ( 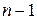) независимых отклонений, ибо по совокупности из 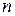единиц после расчета среднего уровня свободно варьируют лишь ( 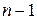) число отклонений.

При расчете объясненной или факторной суммы квадратов 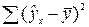используются теоретические значения результативного признака 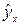, найденные по линии регрессии: .

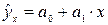В линейной регрессии .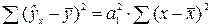

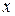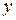Поскольку при определенном объеме наблюдений по и факторная сумма квадратов при линейной регрессии зависит только от одной постоянной – коэффициента регрессии 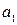, то данная сумма квадратов имеет одну степень свободы. К этому же выводу можно прийти, если рассмотреть составляющие расчетного значения признака .

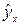Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет ( 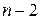). Число степеней свободы для общей суммы квадратов определяется числом единиц, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, то есть 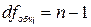. Теперь мы имеем два равенства:

,

.

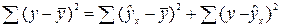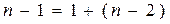Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, дисперсии на одну степень свободы.

,

,

.

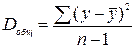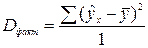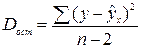Так как это дисперсии на одну степень свободы, их можно сравнивать между собой. Критерии Фишера позволяет проверить нулевую гипотезу 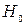о том, что факторная и остаточная дисперсии на одну степень свободы равны между собой 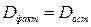. Критерий Фишера рассчитывается по следующей формуле:

.

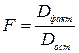Если гипотеза 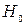подтверждается, то факторная и остаточная дисперсии одинаковы и уравнение регрессии незначимо. Чтобы отвергнуть нулевую гипотезу и подтвердить значимость уравнения регрессии в целом, необходимо, чтобы факторная дисперсия на одну степень свободы превышала остаточную дисперсию на одну степень свободы в несколько раз. Существуют специальные таблицы критических значений Фишера при разных уровнях надежности и различных степенях свободы. Эти таблицы содержат максимальные значения отношения дисперсий, при которых нулевая гипотеза подтверждается. Значение критерия Фишера сравнивается с табличным и на основе этого гипотеза 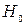принимается или отвергается.

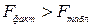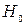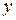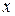Если , тогда гипотеза отклоняется и делается вывод, что связь между и существенна и уравнение регрессии статистически значимо.

Если же 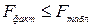, тогда гипотеза 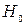принимается и делается вывод, что уравнение регрессии статистически незначимо, так как существует риск (при заданном уровне надежности) сделать неправильный вывод о наличии связи между 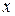и .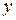

Между 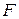-критерием и коэффициентом детерминации существует связь, которую можно выразить через следующую формулу:

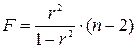
Небольшие расхождения результатов при практических расчетах могут быть связаны с округлением.