Оценка существенности параметров линейной регрессии
В линейной регрессии часто оценивается не только значимость уравнения регрессии в целом, но и значимость отдельных его параметров.
Для того провести такое оценивание, для всех параметров рассчитываются стандартные ошибки: 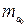 ,
, 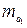 .
.
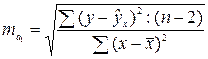 ,
,
Обозначив остаточную дисперсию на одну степень свободы как 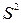 , получим:
, получим:
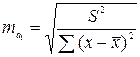 ;
;
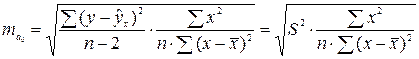 .
.
Величина стандартных ошибок применяется не только для проверки значимости параметров, но и для расчета доверительных интервалов.
Чтобы оценить существенность параметров, необходимо рассчитать для них 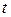 -критерий Стьюдента. Для параметров
-критерий Стьюдента. Для параметров 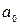 и
и 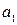
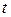 -критерий Стьюдента определяет соотношение между самим параметром и его ошибкой.
-критерий Стьюдента определяет соотношение между самим параметром и его ошибкой.
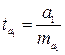 ,
, 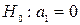 ;
;
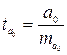 ,
, 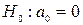 .
.
Фактические значения критерия Стьюдента сравниваются с табличными значениями при определенном уровне надежности 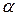 и числе степеней свободы
и числе степеней свободы 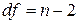 . И на основе этого принимаются или отвергаются нулевые гипотезы о несущественности параметров. Если фактическое значение
. И на основе этого принимаются или отвергаются нулевые гипотезы о несущественности параметров. Если фактическое значение 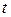 -критерия Стьюдента больше табличного, тогда гипотеза о несущественности отвергается. Подтверждение существенности коэффициента регрессии равнозначно подтверждению существенности всего уравнения регрессии.
-критерия Стьюдента больше табличного, тогда гипотеза о несущественности отвергается. Подтверждение существенности коэффициента регрессии равнозначно подтверждению существенности всего уравнения регрессии.
В парной линейной регрессии между критерием Фишера, критерием Стьюдента коэффициента регрессии, критерием Стьюдента коэффициента корреляции существует связь:
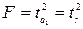 или
или 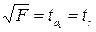 .
.
5. Прогнозирование в линейной регрессии. Интервалы прогноза
После того, как уравнение регрессии построено и проверена его значимость, его можно применять для прогнозирования. С помощью уравнения регрессии можно определить предсказываемое значение результата ( 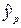 ) при заданном значении фактора
) при заданном значении фактора 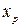 , то есть просто подставить в уравнение регрессии
, то есть просто подставить в уравнение регрессии 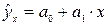 соответствующее значение
соответствующее значение 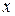 .
.
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом.
Однако вероятность точной реализации такого прогноза крайне мала, поэтому он дополняется расчетом средней ошибкой прогнозирования 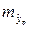 и интервальной оценкой прогнозного значения.
и интервальной оценкой прогнозного значения.
Прогнозируемое значение признака-результата с доверительной вероятностью, равной ( 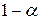 ), принадлежит интервалу прогноза:
), принадлежит интервалу прогноза:
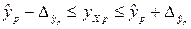
где 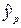 – точечный прогноз;
– точечный прогноз;
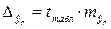 – предельная ошибка прогноза;
– предельная ошибка прогноза;
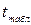 – коэффициент доверия, определяемый по таблицам распределения Стьюдента в зависимости от уровня значимости
– коэффициент доверия, определяемый по таблицам распределения Стьюдента в зависимости от уровня значимости 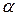 и числа степеней свободы (
и числа степеней свободы ( 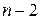 );
);
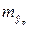 – средняя ошибка прогноза.
– средняя ошибка прогноза.
Средняя ошибка прогнозируемого значения результата составит:
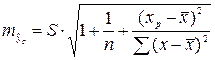
Дата добавления: 2016-05-25; просмотров: 733;
