Модель отказов установок при последовательном соединении элементов

Простейшей системой с точки зрения теории на­дежности является такой комплект элементов, при котором отказ одного элемента вызывает отказ всей системы, но не изменяет надежность других элементов. Такую структуру в теории надежности называют системой с последовательным соединением элементов.

При разработке модели надежности без учета восстановления надежность каждого элемента системы ЭСН можно характеризовать коэффициентом готовности Кг (вероятность рабочего состояния р) и коэффициентом вынужденного простоя Кв (вероятность состояния отказа q). Если не учитывать плановые простои (ремонты), то можно считать, что элемент в любой момент времени находится в одном из этих состояний. Тогда сумма вероятностей этих состояний равна 1:

p + q = 1. (3.7)

Для группы из двух элементов возможны следующие сочетания:

— оба элемента в рабочем состоянии;

— первый элемент в вынужденном простое, второй в рабочем состоянии;

— первый элемент в рабочем состоянии, второй в вынужденном простое;

— оба элемента в вынужденном простое.

Вероятности этих состояний можно найти, воспользовавшись теоремой умножения вероятностей событий. Применительно к состояниям элементов теорема умножения может быть сформулирована следующим образом: вероятность сложного события, состоящего в совпадении данных независимых состояний группы элементов, равна произведению вероятностей этих состояний. [8]

Тогда вероятность сложного события группы из двух элементов, когда оба элемента находятся в рабочем состоянии, будет равна произведению вероятностей этих состояний:

(p1 + q1) (p2 + q2) = p1p2+ q1p2 + p1q2 + q1q2= 1. (3.8)

Если в системе из двух элементов элементы резервируют друг друга, то отказ системы произойдет только тогда, когда откажут оба:

qc = q1 q2 (3.9)

А вероятность надежной работы в этом случае:

pc = 1 – qc = 1 – q1q2 = p1p2+ q1p2 + p1q2. (3.10)

Таким образом, вероятность надежной работы системы из двух взаиморезервируемых элементов можно определить, пользуясь теоремами сложения и умножения вероятностей. Теорема сложенияформулируется так: вероятность состояния группы элементов, состоящего в появлении хотя бы одного из заданных несовместимых состояний, равна сумме вероятности этих состояний. [8]

Если два элемента не резервируют друг друга, то состояние отказа этой системы будет тогда, когда откажет хотя бы один элемент, а состояние надежной работы будет тогда, когда оба элемента в работе, т.е. для не резервированной системы из двух элементов вероятность надежной работы:

pc = p1 p2 (3.11)

А вероятность отказа в данном случае:

qc = 1 – pc = 1 – p1p 2 = q1q2+ q1p2 + p1q2. (3.12)

Для анализа показателей надежности электрической схемы соединений элементов или ее части используют структурные (логические) схемы надежности, которые учитывают электрическую схему, резервирование элементов и влияние их отказов на отказ всей системы. Например, если система состоит из двух элементов, и отказ элемента не приводит к отказу всей системы, то в логической схеме элементы соединяются параллельно. Если отказ одного из элементов приводит к отказу всей системы, то эти элементы соединяются последовательно.

Отметим, что логическая схема надежности не всегда совпадает с электрической схемой, особенно для схем с большим количеством присоединений.

Эта система будет находиться в рабочем состоянии, если все элементы находятся в рабочем состоянии. Сложное событие — работа всех элементов схемы состоит в совмещении событий работы каждого элемента. Применяя теорему умножения вероятностей независимых событий, получаем вероятность безотказной работы системы как произведение вероятностей безотказной работы всех элементов:

pc = p1p2p3 … pn= 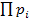, (3.13)

где i = 1,2, ..., n — элементы в последовательно соединенной системе;

pi — вероятность безотказной работы i-го элемента.

Вероятность состояния отказа определяется как вероятность события, противоположного рабочему состоянию:

qc = 1 — pc= 1 — 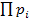, (3.14)

На практике вероятность состояния отказа в последовательно соединенной системе определяется как вероятность отказа хотя бы одного элемента, которая определяется с использованием формулы для вероятностей суммы совместных событий:

qc = 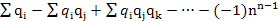q1 qn. (3.15)

Для элементов электрических систем вероятности отказов гораздо меньше 1, поэтому при определении состояния отказа из n последовательно соединенных элементов вторым, третьим и последующими слагаемыми правой части равенства (3.15) можно пренебречь, как числами более высокого порядка малости. Поэтому в практических расчетах используют формулу:

При последовательном соединении элементов в логической схеме надежности вероятности безотказной работы элементов перемножаются (3.13), поэтому при экспоненциальном законе распределения:

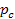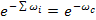= (3.17)

Отсюда параметр потока отказов при последовательном соединении определяется как:

Следовательно, чем большее число элементов n соединено последовательно в логической схеме надежности, тем больше параметр потока отказов системы и тем меньше вероятность ее надежной работы.

Среднее время между отказами или время наработки на отказ для схемы из n элементов равно:

Tср = 1/ωc = 1/ 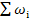= 1/(1/T1 + 1/T2 +…+1/Tn). (3.19)

Если известны вероятность вынужденного простоя и параметр потока отказов, можно определить среднее время одного восстановления (аварийного ремонта) системы в долях года:

Tв.с. = qc /ωc. (3.20)

В случае последовательного соединения 2-х элементов и при критерии — выход из работы любого элемента нарушает технологическую связь между входом А и выходом В (случай отказа) — эквивалентные показатели надёжности рассчитываются по формулам:

— интенсивность (параметр) потока отказов:

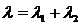; (3.21)

— среднее время восстановления:

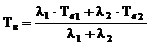. (3.22)

Структурой из последовательно соединенных элементов можно моделировать надежность электрических цепей с последовательным соединением аппаратов, трансформаторов, проводов, кабелей и ВЛ, а также схем, содержащих обмотки и контакты реле, резисторы, тиристоры, катушки индуктивности и электронные приборы.

В качестве примера рассмотрим участок электрической сети, состоящей из последовательно соединенных элементов: выключателя, ЛЭП и трансформатора (рисунок 3.1). Очевидно, что отказ любого из элементов приводит к вынужденному простою всего участка. Влияние каждого из элементов на надежность всего участка можно оценить поданным таблице 3.2, где приведены показатели надежности элементов участка сети напряжением 110 кВ.

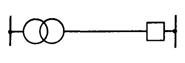
Рисунок 3.1 – Схема ЛЭП

Таблица 3.2 — Показатели надежности элементов участка сети напряжением 110 кВ

Сопоставление параметров потоков отказов ω элементов каждого из напряжений показывает, что наименее надежным элементом являются ЛЭП. Их параметр потока отказов на порядок больше параметров потока отказов трансформаторов и выключателей.

Время восстановления Тср трансформаторов и выключателей, наоборот, на порядок больше, чем у ЛЭП. Это приводит к тому, что значения коэффициентов вынужденного простоя Кв (вероятности отказов) всех элементов имеют одинаковый порядок.

Рассмотрим простейшую схему электрических соединений, состоящую из выключателя, ЛЭП и трансформатора (рисунок 3.1) [8]. Для такой электрической схемы логическая схема надежности представляет собой последовательное соединение трех элементов, так как отказ любого элемента вызывает отказ всей системы. На рисунке 3.2 дана соответствующая логическая схема надежности. Обычно над прямоугольником, отражающим влияние каждого элемента на надежность системы в целом, указываются вид элемента, а в прямоугольнике — присвоенный ему номер в схеме надежности.

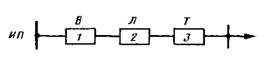
Рисунок 3.2 — Логическая схема надежно сети ЛЭП

Если шины ИП, от которого отходит линия, имеют еще присоединения (рисунок 3.3), то их надежность отражается на надежности ЭСН потребителей рассматриваемой линии, поскольку отказ или вывод в плановый ремонт каждого из шинных разъединителей приводит к отключению всей шины и, следовательно, к отключению рассматриваемой линии.

Поскольку, как сказано выше, отказ каждого присоединения приводит к отказу всей системы, в логической схеме надежности эти элементы соединены последовательно с элементами рассматриваемой линии (рисунок 3.4).

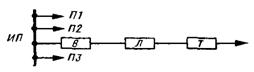
Рисунок 3.3 — Схема ЛЭП с несколькими (тремя) присоединениями к шинам ИП

Рисунок 3.4 — Логическая схема надежности ЛЭП с

тремя присоединениями к шинам ИП

Очевидно, что значение параметра потока отказов схемы на рисунке 3.4 больше, чем схемы на рис. 3.2, и чем большее число присоединений имеют шины ИП, тем менее надежна система ЭСН в целом.