Процесс ортогонализации.
Пусть 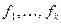 линейно не зависимая система векторов. Следующий процесс позволяет строить эквивалентную ей ортогональную систему векторов:
линейно не зависимая система векторов. Следующий процесс позволяет строить эквивалентную ей ортогональную систему векторов:
Положим 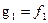 ,
,  , …,
, …, 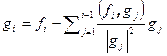 … . Процесс не может быть продолжен только в случае, когда
… . Процесс не может быть продолжен только в случае, когда 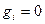 . Но тогда
. Но тогда 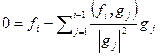 , и, значит,
, и, значит, 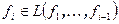 , что противоречит линейной независимости исходной системы векторов.
, что противоречит линейной независимости исходной системы векторов.
Ортогональность построенной системы проверяется непосредственно. Допустим, ортогональность системы векторов 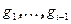 установлена. Покажем, что вектор
установлена. Покажем, что вектор 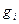 ортогонален всем векторам, построенным ранее него. Действительно,
ортогонален всем векторам, построенным ранее него. Действительно, 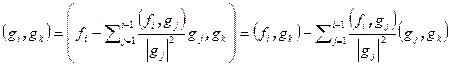 , где k=1,2,…i-1. В силу ортогональности системы векторов
, где k=1,2,…i-1. В силу ортогональности системы векторов 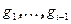 в сумме из правой части равенства только одно не нулевое слагаемое, получаемое при j=k. Следовательно,
в сумме из правой части равенства только одно не нулевое слагаемое, получаемое при j=k. Следовательно, 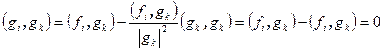 .
.
Следствие 2.1 В любом подпространстве конечномерного евклидова пространства имеется ортогональный базис.
Доказательство. Возьмем базис подпространства и применим к нему процесс ортогонализации. В результате будет построена ортогональная система векторов (а, значит, и линейно независимая) из этого подпространства. Поскольку количество векторов в построенной системе совпадает с размерностью подпространства, то, следовательно, построенная ортогональная система векторов является базисом подпространства.
Следствие 2.2. Любую ортогональную систему векторов можно дополнить до ортогонального базиса всего пространства.
Доказательство. Пусть 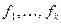 - ортогональная система векторов. Дополним ее до базиса всего пространства векторами
- ортогональная система векторов. Дополним ее до базиса всего пространства векторами 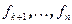 и к полученной системе
и к полученной системе 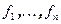 применим процесс ортогонализации. В результате будет построен ортогональный базис
применим процесс ортогонализации. В результате будет построен ортогональный базис  всего пространства. Поскольку первые k векторов были ортогональны, то в процессе ортогонализации они не изменились, т.е.
всего пространства. Поскольку первые k векторов были ортогональны, то в процессе ортогонализации они не изменились, т.е. 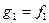 ,…,
,…,  . Таким образом, векторы
. Таким образом, векторы 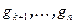 дополняют ортогональную систему
дополняют ортогональную систему 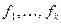 до ортогонального базиса всего пространства.
до ортогонального базиса всего пространства.
Следствие 2.3. Пусть 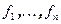 - базис пространства, а
- базис пространства, а  - ортогональный базис пространства, полученный из базиса
- ортогональный базис пространства, полученный из базиса 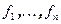 процессом ортогонализации. Тогда матрица перехода от одного базиса к другому является треугольной, и на ее главной диагонали стоят 1.
процессом ортогонализации. Тогда матрица перехода от одного базиса к другому является треугольной, и на ее главной диагонали стоят 1.
Доказательство. Согласно процессу ортогонализации имеем 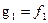 ,
, 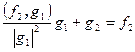 , …,
, …,  …, а, значит, матрица перехода P (ее столбцы – координаты базисных векторов) равна
…, а, значит, матрица перехода P (ее столбцы – координаты базисных векторов) равна 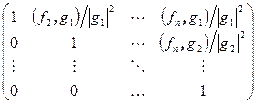 .
.
Дата добавления: 2016-05-25; просмотров: 1126;
