Скалярное произведение.
Геометрия на плоскости и в пространстве.
Целью данного раздела состоит в рассмотрении таких геометрических понятий как расстояние, площадь, объём с последующим обобщением этих понятий и их переносом на произвольные линейные пространства.
Скалярное произведение.
Определение 1.1. Скалярным произведением геометрических векторов a и b называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение векторов обозначают 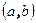 .
.
Из определения следует, что длина вектора равна 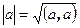 .
.
Приведём свойства скалярного произведения.
1.  . Симметричность
. Симметричность
2. 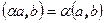 Линейность
Линейность
3. 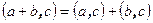
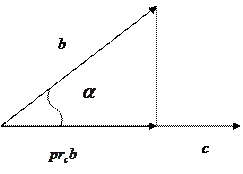
В доказательстве нуждается только третье равенство. Если c=0, то равенство очевидно. Пусть  . Проекция вектора b на c равна
. Проекция вектора b на c равна 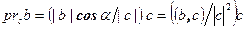 .
.
 Из равенства
Из равенства 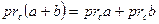 и приведённой выше формулы выводим
и приведённой выше формулы выводим 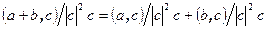 . Приравняем коэффициенты при векторе c в левой и правой частях равенства
. Приравняем коэффициенты при векторе c в левой и правой частях равенства 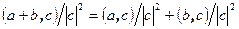 и умножим на квадрат длины вектора c, получим свойство 3.
и умножим на квадрат длины вектора c, получим свойство 3.
Задание длин векторов определяет скалярное произведение. Действительно, из свойств скалярного произведения выводим равенство 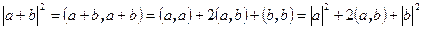 , которое перепишем в виде
, которое перепишем в виде
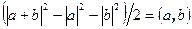 . Таким образом, задание длин векторов равносильно заданию скалярного произведения и наоборот.
. Таким образом, задание длин векторов равносильно заданию скалярного произведения и наоборот.
Выразим скалярное произведение через координаты перемножаемых векторов. Пусть 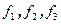 - базис пространства векторов, и
- базис пространства векторов, и 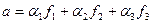 ,
, 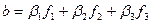 - разложения векторов a,b по этому базису. Тогда по свойствам скалярного произведения выводим
- разложения векторов a,b по этому базису. Тогда по свойствам скалярного произведения выводим 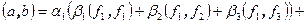
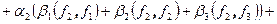
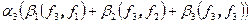 . Обозначим через
. Обозначим через 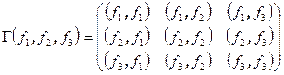 матрицу Грамма от векторов
матрицу Грамма от векторов 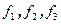 , составленную из скалярных произведений этих векторов, через
, составленную из скалярных произведений этих векторов, через  - координаты вектора a в базисе f. В этих обозначениях скалярное произведение можно записать с помощью матричных операций следующим образом
- координаты вектора a в базисе f. В этих обозначениях скалярное произведение можно записать с помощью матричных операций следующим образом 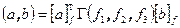 .
.
Векторы называются ортогональными (перпендикулярными) если угол между ними равен 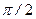 . Условие ортогональности векторов равносильно равенству нулю их скалярного произведения.
. Условие ортогональности векторов равносильно равенству нулю их скалярного произведения.
Базис  называется ортогональным, если базисные векторы попарно ортогональны. Матрица Грамма ортогональной системы векторов – диагональная. Выражение скалярного произведения через координаты векторов в ортогональном базисе принимает более простой вид, а именно,
называется ортогональным, если базисные векторы попарно ортогональны. Матрица Грамма ортогональной системы векторов – диагональная. Выражение скалярного произведения через координаты векторов в ортогональном базисе принимает более простой вид, а именно, 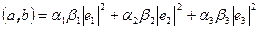 .
.
В ортогональном базисе скалярное произведение вектора a на базисный вектор равно 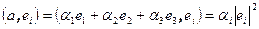 , то есть, координаты вектора a находятся по формулам
, то есть, координаты вектора a находятся по формулам 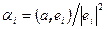 .
.
Ортогональный базис 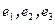 , в котором длина каждого базисного вектора равна 1, называется ортонормированным. В ортонормированном базисе координаты вектора x определяются по формулам
, в котором длина каждого базисного вектора равна 1, называется ортонормированным. В ортонормированном базисе координаты вектора x определяются по формулам 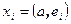 , а скалярное произведение векторов равно
, а скалярное произведение векторов равно 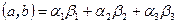 .
.
Дата добавления: 2016-05-25; просмотров: 621;
