ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ

При решении линейных неоднородных дифференциальных уравнений можно использовать метод подбора частного решения и метод вариации произвольных постоянных (метод Лагранжа). Каждый метод имеет свою сферу применимости, достоинства и недостатки. Ниже приведены описания методов, сопровожденные примерами.

Метод подбора частного решения

Рассмотрим линейное неоднородное уравнение n-го порядка с действительными числовыми коэффициентами

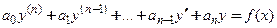. (10)

Если правая часть 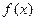уравнения имеет вид

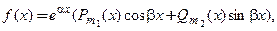(11)

где многочлены по степеням и их старшие степени, то уравнение (10) называют дифференциальным уравнением со специальной правой частью, а функцию 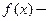квазимногочленом, или квазиполиномом. Можно доказать, что частное решение 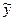уравнения (10) также представимо в виде квазимногочлена:

(12)

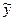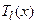Как следует из записи, частное решение содержит два новых параметра и два многочлена и 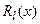с неизвестными коэффициентами, подлежащих определению.

Параметр 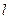равен наибольшей из степеней многочленов и .

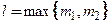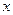Чтобы найти параметр , нужно составить вспомогательное комплексное число в котором коэффициенты при в функциях ,

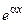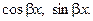
Если число не совпадает ни с одним корнем характеристического уравнения (7) для соответствующего линейного однородного уравнения n-го порядка (6), то полагают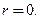

Если число совпадает с каким-либо корнем характеристического уравнения, то 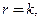где кратность этого корня. Кратко можно описать так:

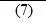
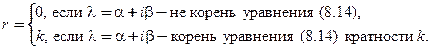
Многочлены 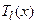и 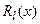имеют одинаковую степень 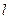. Чтобы найти эти многочлены, нужно записать их с неопределенными коэффициентами:

(13)

Затем частное решение 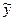, составленное по формуле (12), подставляют в (10), и из условия тождественного равенства левой и правой части уравнения находят коэффициенты и этих многочленов.

Общее решение линейного неоднородного уравнения по формуле (5) представляют в виде

Алгоритм 2 решения линейного неоднородного уравнения с постоянными коэффициентами и специальной правой частью

1. Найти общее решение соответствующего линейного однородного уравнения (применить алгоритм 1).

2.Методом подбора найти частное решение 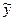заданного линейного неоднородного уравнения (применить формулу (12)).

3. Составить общее решение линейного неоднородного уравнения по формуле

.

Метод вариации произвольных постоянных (метод Лагранжа)

Рассмотрим линейное неоднородное уравнение n-го порядка с коэффициентами 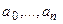, являющимися действительными функциями переменной х:

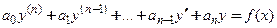. (14)

Пусть для соответствующего линейного однородного уравнения n-го порядка известна фундаментальная система решений . Тогда согласно методу вариаций произвольных постоянных решение линейного неоднородного уравнения представимо в виде

(15)

где 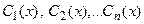− неизвестные наперед функции, удовлетворяющие системе уравнений:

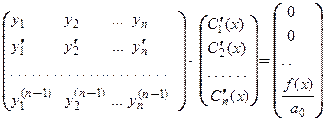. (16)

Эту систему можно рассматривать как систему линейных алгебраических уравнений относительно производных . Система имеет единственное решение, так как ее определитель равен определителю Вронского, который отличен от нуля в силу фундаментальности системы функций . Из системы (16) найдем , а затем, интегрируя найденные выражения для производных, найдем и сами функции 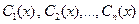. Подставим их в (15) и получим решение.

Метод вариации произвольных постоянных позволяет построить как частное, так и общее решение линейного неоднородного уравнения. Если при интегрировании выражений для производных постоянным 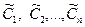придать конкретные числовые значения, то получим по формуле (15) частное решение. Если постоянные не фиксировать, то формула (15) даст общее решение.

Проиллюстрируем описанный метод на примерах.

Пример 2. Решить уравнение

□ Данное уравнение является линейным неоднородным уравнением 2-го порядка с постоянными коэффициентами. Сравнивая с (14), получаем: . К этому уравнению не применим метод подбора частного решения, так как правая часть не является квазимногочленом. Воспользуемся методом вариации произвольных постоянных. Однородное уравнение, соответствующее данному линейному неоднородному уравнению, имеет вид Его фундаментальная система решений состоит из двух функций . В соответствии с методом Лагранжа запишем решение линейного неоднородного уравнения в виде (15):

.

Функции 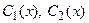удовлетворяют системе (16):

Интегрируем правые части:

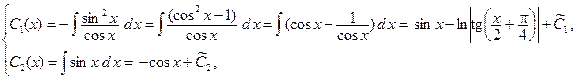
где − произвольные постоянные.

Подставляем функции в общее решение линейного неоднородного уравнения:

.

Как видим, общее решение неоднородного уравнения является суммой общего решения соответствующего однородного уравнения и функции 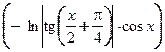, являющейся частным решением неоднородного уравнения. ■