Теплоемкость жидкостей. Простые закономерности для теплоемкостей идеальных газов не могут быть справедливыми для реальных газов и тем более для жидкостей

Простые закономерности для теплоемкостей идеальных газов не могут быть справедливыми для реальных газов и тем более для жидкостей, так как их внутренняя энергия опреде­ляется не только кинетической энергией теплового движения молекул, но и потенциальной энергией их взаимодействия. Внутренняя энергия жидкостей зависит от температуры и от ее объема U = U(T, V). С учетом этой зависимости запишем первое начало термодинамики δQ = dU + δА в виде

.

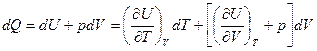Из этого уравнения определим молярную теплоемкость жидкости при постоянном давлении

.

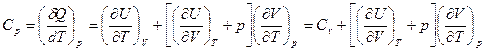где С_V — молярная теплоемкость при постоянном объеме;

.

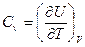Как видно из формулы (21.4), для жидкостей С_р — C_v ≠ R,так как входящее в эту формулу изменение внутренней энер­гии в зависимости от объема отлично от нуля.

Термодинамический расчет дает для любого тела общее соотношение

,

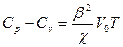где Vo — объем моля; β — коэффициент теплового расширения; χ — коэффициент сжимаемости (см. формулы (20.1) и (20.2)).

Для жидкостей в зависимости от значения β и величины сил межмолекулярного взаимодействия в большей или мень­шей степени С_р—C_v превосходит R (для газов С_р — C_V 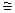R).

У подавляющего числа жидкостей теплоемкость с повыше­нием температуры растет, у других наоборот уменьшается (ртуть). Может быть и более сложная зависимость тепло­емкости: так, для воды теплоемкость сначала с повышением температуры (от 0°С) падает, а затем, после прохождения минимума существенно возрастает.

Численные значения теплоемкостей жидкостей могут быть самыми разнообразными. Для большинства металлов, напри­мер, молярная теплоемкость обычно близка к значению 3R (R — универсальная газовая постоянная).

Диффузия

Явления переноса в жидкостях можно описывать теми же уравнениями (19.8), (19.16), (19.19), что и соответствующие процессы в газах, но при этом коэффициенты диффузии, теп­лопроводности и внутреннего трения (D, χ, η)выражаются иными соотношениями. Диффузия в жидкостях происходит значительно медленнее, чем в газах, поскольку обусловлена только перескоками молекул: молекула жидкости может вре­мя от времени в результате случайных взаимодействий с со­седними молекулами покинуть положение равновесия и «скачком» перейти в другое.

В результате взаимодействия с соседями энергия молеку­лы может возрасти по сравнению с ее средним значением при данной температуре Т. Обозначим энергию, необходимую молекуле для «скачка» — перемены «места жительства», через ε (энергия активации). Согласно распределению Больцмана (18.36), число молекул, меняющих место жительства, будет

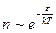. (21.5)

При данной температуре доля «кочующих» молекул неве­лика (менее 0,1%). С увеличением температуры, согласно формуле (21.5), число «кочующих» молекул заметно возра­стает.

Согласно Я. И. Френкелю, время релаксации 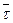«оседлой» молекулы связано с периодом Т₀ их колебания около поло­жения равновесия соотношением:

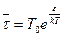. (21.6)

За время релаксации 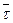молекула продвигается в среднем на расстояние 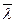. С учетом формулы (21.6) получаем значение средней скорости

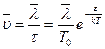. (21.7)

Коэффициент диффузии однородной жидкости выражает­ся формулой, аналогичной формуле для газов

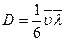
или с учетом (21.7) получим:

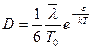. (21.8)

Как видно из последней формулы, коэффициент диффузии с возрастанием температуры резко увеличивается. Это объяс­няется уменьшением времени релаксации, увеличением 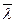и 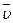. (В жидком состоянии коэффициент диффузии в 10⁴ ... 10⁵ раз меньше, чем у газов, но в 10²⁰ больше, чем в твердом.)