Смачивание. Давление под изогнутой поверхностью. Капиллярные явления

При соприкосновении жидкости с твердым телом возмож­ны два случая: 1) силы взаимодействия между молекулами жидкости меньше, чем силы взаимодействия между молеку­лами жидкости и твердого тела; 2) силы взаимодействия ме­жду молекулами жидкости больше сил взаимодействия между молекулами жидкости и твердым телом. В первом случае имеет место смачивание, во втором — несмачивание. Благодаря поверхностному натяжению, под поверхностью жидкости возникает молекулярное давление, которое приближенно оп­ределяется формулой Ван-дер-Ваальса 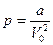. где а — константа, зависящая от типа жидкости; V₀ — молярный объем. Это давление может достигать тысяч атмосфер. Если поверх­ность жидкости изогнутая, то возникает добавочное давление р_д (соответственно отрицательное или положительное в зави­симости от вогнутости или выпуклости поверхности).

Определим добавочное давление р_д для сферической по­верхности жидкости. Мысленно рассечем сферическую каплю жидкости радиуса R по диаметру на два полушария.

Каждое из полушарий притягивается друг к другу с силой поверхностного натяжения

F = α∙2πR.

Эта сила прижимает каждое полушарие к поверхности се­чения капли S = πR², создавая дополнительное давление р_д:

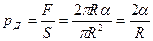. (21.1)

Если поверхность жидкости имеет более сложную форму, то р_допределяется формулой Лапласа:

,

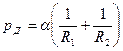где R₁ и R₂ — радиусы кривизны двух взаимно перпендику­лярных нормальных сечений поверхности.

Благодаря смачиванию, поверхность жидкости, находя­щейся в узкой трубке, принимает вогнутую форму.

Для количественной характеристики явления смачивания вводится краевой угол. Краевой угол θ — угол, образованный касательными к поверхности жидкости и твердого тела в ме­сте их контакта. Краевой угол проводится так, чтобы жид­кость была внутри краевого угла (рис. 22.1).

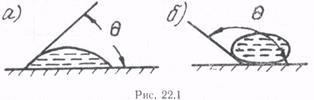
При смачивании краевой угол — острый, капля жидкости растягивается по поверхности тела (рис. 22.1, а). В идеаль­ном случае полного смачивания θ = 0. При несмачивании краевой угол — тупой (рис. 22.1,6). При полном несмачива­нии θ = π.

Будет ли наблюдаться смачивание или несмачивание, за­висит от сочетания энергетических характеристик контактов пар «жидкость — твердое тело». Одна и та же жидкость сма­чивает одни тела и не смачивает другие (вода смачивает стек­ло, не смачивает воск; ртуть смачивает золото, не смачивает стекло).

Из-за смачивания или несмачивания жидкостью твердого тела вблизи стенок сосуда, в котором находится жидкость, граничащая с газом или паром, наблюдается искривление по­верхности жидкости. В узком зазоре между двумя стенками или в узкой трубке (именуемой капилляром) искривляется вся поверхность, принимая вогнутую (рис. 22.2, а, смачива­ние) или выпуклую (рис. 22.2, б, несмачивание) форму. Тако­го рода поверхности называются менисками.

В капиллярной трубке, опущенной одним концом в жид­кость, под образующимся мениском появляется либо отрица­тельное (смачивание, рис. 22.2, а), либо положительное (не­смачивание, рис. 22.2, б)добавочное давление р_д.

Рассмотрим капилляр радиуса r (r = KK′), опущенный одним концом в смачиваемую жидкость (рис. 22.2, а). Благо­даря отрицательному добавочному давлению р_д, под вогну­тым мениском жидкость поднимется на высоту h. Между жидкостью в широком сосуде и в капилляре установится

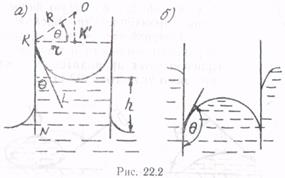
некоторая разность уровней h. В условии равновесия гидро­статическое давление жидкости

p = ρgh, (21.2)

где ρ — плотность жидкости; g —ускорение свободного паде­ния (уравновешивается отрицательным давлением мениска p_д: p = p_д). Подставив в это равенство значения р и р_д из формул (21.1) и (21.2), получим

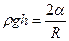,(21.3)

где R — радиус кривизны мениска.

На рис. 22.2 краевой угол обозначен через θ, он образован касательной KL к поверхности жидкости и стенкой сосуда KN. Поскольку радиус мениска ОК == R перпендикулярен ка­сательной KL, то очевидно угол ОКК' = 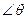. Поэтому радиус мениска R и радиус капилляра r связаны с краевым углом соотношением 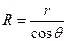. С учетом этого соотношения и формулы (21.3) для высоты подъема жидкости в капилляре получим

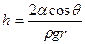(уравнение Лапласа).

Чем меньше r, тем больше высота подъема, поэтому под­нятие смачивающей жидкости особенно заметно в узких труб­ках-капиллярах, в которых жидкость способна подниматься на десятки метров.

Капиллярные явления играют большую роль в живой и неживой природе, технике, быту. Капиллярные явления облег­чают всасывание влаги растениями, поднимают воду в почве, кровеносные капиллярные сосуды живых существ обеспечивают все участки организма кровью; если между фундамен­том и стенами строящегося здания не проложить слой гидро­изоляции, то влага из почвы будет подниматься по капилля­рам кирпичей, что приведет к насыщению водой строительных материалов и снижению их прочности, а также к дополни­тельному притоку паров воды в помещения.

Предельные размеры радиусов r трубок, которые еще можно считать капиллярами, определяются соотношением (21.3). Из этого соотношения следует, что для воды r_к ≤ 0,1 мм.

В природе встречаются капилляры с радиусами до 10^-4 мм.