Теплопроводность жидкостей

По сравнению с газами коэффициенты теплопроводности жидкостей выражаются более сложными формулами. В явле­нии теплопроводности перескоки молекул заметной роли не играют; теплопроводность обусловлена обменом кинетиче­ской энергией колеблющихся частиц.

Колеблющиеся частицы образуют тепловые волны звуковых частот. Квантовая теория таким волнам сопоставляет квазичастицы — фононы, движение которых и обуславливает перенос энергии через жидкость, т. е. теплопроводность.

Увеличение температуры уменьшает силы притяжения между молекулами. Поэтому в отличие от газов коэффициен­ты теплопроводности с увеличением температуры уменьшают­ся. Изменение давления на значениях коэффициентов тепло­проводности практически не сказывается. Теплопроводность жидкостей выше, чем газов в ~ 10² раз.

Вязкость жидкостей

Вязкость жидкости на один — три порядка больше вязко­сти их паров и очень сильно зависит от температуры. При температурах, близких к критической, вязкость жидкости приближается к вязкости ее насыщенного пара. Но с пони­жением температуры вязкость возрастает и у переохлажден­ных жидкостей достигает огромных величин. В результате переохлажденная жидкость становится твердым телом, не переходя в кристаллическое состояние (стекло). Уменьшение температуры увеличивает время релаксации 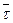, молекулы реже изменяют свои положения равновесия, что сказывается на коэффициенте вязкости, увеличивая его. Как следует из теории и подтверждается практикой,— коэффициент вязко­сти ηпрямо пропорционален τ, поэтому η, так же как и 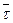(21.6), должен зависеть от температуры, возрастая с пониже­нием температуры по экспоненциальному закону:

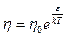, (21.9)

где η₀ — коэффициент, зависящий от химической природы ве­щества и практически независящий от температуры. Формула (21.9) была получена Я. И. Френкелем, который рассматри­вал вязкость жидкости как результат миграции молекул. По­стоянные η₀и ε определяются экспериментально.

А. И. Бачинский, рассматривая вязкость как результат силового взаимодействия молекул, получил для коэффициента вязкости формулу

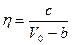, (21.10)

где V₀ — молярный объем; b — собственный объем молекул при их плотной упа­ковке (постоянная уравнения состояния Ван-дер-Ваальса); с — константа, зависящая от химической природы жид­костей.

Константы с и b, так же как и величины η₀ и ε, опреде­ляются экспериментально. Формулы (21.9) и (21.10) выпол­няются не во всей области температур существования жид­кого состояния вещества.

Зависимость вязкости от давления проявляется практиче­ски лишь в области очень высоких давлений, где вязкость с ростом давления быстро возрастает, что объясняется воз­растанием энергии активации ε и временем релаксации .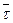

Для практической деятельности существенен характер те­чения жидкости в тех или иных условиях. Особенности тече­ния жидкости зависят от ее плотности ρ и динамической вяз­кости η. Кроме того, необходимо знать характерные для дан­ного исследования скорость течения υ и линейный, характе­ризующий систему, размер r, например, для движения жид­кости в трубе: характерная скорость υ— средняя скорость по­тока, линейный размер r — радиус трубы. Эти параметры оп­ределяют число Рейнольдса

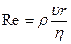. (21.11)

Число Рейнольдса позволяет определить характер течения. Течение жидкости или газа может быть ламинарным, нося­щим слоистый характер, или турбулентным, при котором на­блюдаются вихреобразные движения среды. Течение любой жидкости в зависимости от скорости, формы и размеров канала можно охарактеризовать критическим значением числа Рейнольдса Re_K. Если для данного течения Re <Re_K, то воз­можно только ламинарное течение, при Re > Re_K возникает турбулентное движение (появляются вихри). Обычно числен­ное значение Re_K определяют опытным путем.

Особое значение число Рейнольдса играет в инженерной практике. Оказывается, течения различных сред в каналах будут подобными, если числа Re для них одинаковы. (Подоб­ными называются движения, которые отличаются только мас­штабами своих характеристик.) Поэтому можно выяснить по­ведение потока воздуха при обтекании самолета; воды, обте­кающей корабль; поведение воды в турбине электростанции, проводя испытания на моделях, для которых числа Re соот­ветствуют реальным процессам.