Задача 1. Оценка общей информативности изображения

Исходные предпосылки

Совместная информация, содержащаяся в изображении трех каналов, есть

Н(R,B,G) = H(R)+H(B)+H(G) –T(R,B,G), где

H(R),(H(B),H(G)) – энтропия (разнообразие) в канале R – красный (B – голубой, G – зеленый).

T(R,B,G) – сопряженность между каналами.

H(R) = -Sp(r_i)log(p(r_i)),

где r_i – i- значение яркости красного канала,

H(R,G,B)= -Sp(r_i,g_i,b_i)log(p(r_i,g_i,b_i)) –

информация, содержащаяся в трех каналах друг о друге, или мера сопряженности [Кульбак, 1956].

Если каналы полностью не зависят друг от друга, то сумма их частных энтропий равна совместной энтропии, если же они как-то сопряжены друг с другом, то совместная энтропия меньше этой суммы. Прямое определение сопряженности трех каналов практически невозможно даже для очень больших объемов данных, так как требует очень большого числа степеней свободы. Измерения в каждом канале обычно имеют 256 градаций яркости, и, соответственно, для оценки совместной сопряженности требуется примерно 256³ измерений. Задачу можно решить, если разложить трехмерное изображение по независимым ортогональным составляющим – компонентам. Затем для каждой независимой компоненты определить энтропию и суммировать эти энтропии с учетом веса компоненты. Покажем последовательно решение этой задачи.

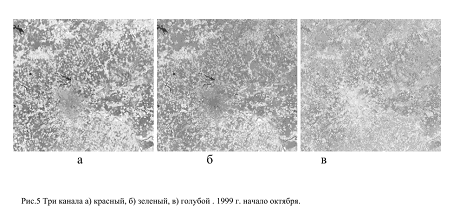
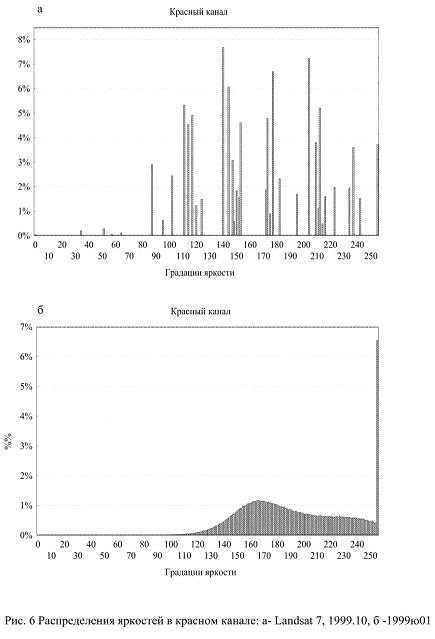
На рис. 5 показано изображение, разложенное на три канала, а на рис. 6 – распределение яркостей по частотам в красном канале. Следует отметить, что используемое осеннее изображение (рис.4 а) представлено в Интернете в сжатом виде. В результате распределение яркостей не охватывает всей амплитуды возможных значений. Этот дефект весьма удобен для демонстрации подхода, обеспечивающего соизмеримость оценок по изображениям различного качества.

Для ортогонального преобразования многоканальных изображений обычно используют метод главных компонент. В первом приближении его действие можно определить следующим образом: допустим, что изображения в трех каналах полностью подобны друг другу. Тогда корреляция между ними будет равна 1, и значения яркости во всех трех каналах можно рассматривать как зависящие от одного фактора. В противоположной ситуации, когда каналы полностью независимы, каждый из них описывается собственным независимым фактором.

Если же реально яркости в каналах в какой-то степени коррелируют друг с другом, то ситуация промежуточная, и эти каналы можно отобразить как функции от трех независимых факторов. Задача расчета независимых ортогональных факторов решается на основе матричной алгебры.

Приведем статистические параметры для трех каналов и их факторное отображение.

Таблица 1