Задача 2. Анализ иерархической организации и его разнообразия
Исследование иерархии географического пространства – наиболее активно развивающееся направление. За последние 10 лет в мировой науке для решения этой задачи развит широкий арсенал количественных методов с применением теории фракталов, спектрального анализа, вейвлет анализа. Суть задачи сводится к выявлению правил, порождающих иерархию, и использованию этих правил для решения практических задач согласования изображений на картах различного масштаба, выбора масштаба для составления ландшафтных карт различного целевого назначения и, наконец, для создания основы для изучения и описания механизмов, порождающих иерархию. К настоящему времени этой теме посвящена огромная литература, с которой достаточно полно можно познакомится через Интернет (Приложение № 2 ). Вместе с тем следует отметить, что исследование иерархии требует от молодого специалиста базовых знаний статистики и основ анализа временных рядов. В данном случае теоретические основания анализа будут изложены на самом общем понятийном уровне.
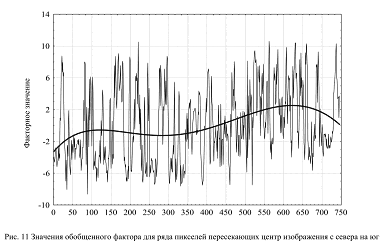
В основе исследования иерархии фактически лежит постулируемая Л. С. Бергом цель географии: «Целью географического исследования является отыскание связей и закономерностей, какие существуют между распространением отдельных, интересующих географа вещей…» [Л. С. Берг, 1958, стр. 116]. Для того чтобы последовательно разобрать ход такого исследования, вырежем из изображения, компилированного из шести факторов (рис. 10) рассматриваемого изображения, линию пикселей со значениями фактора, проходящую с севера на юг через центр изображения (рис. 11). Компилированное изображение строится как сумма значений всех шести факторов с весом каждого, пропорциональным его дисперсии. Так как факторы по условию независимы, такая сумма содержит всю информацию о структуре территории.
Из рис. 11 видно довольно резкое варьирование значений обобщенного фактора, отражающее изменение состояния подстилающей поверхности. При этом полиномиальный тренд (черная линия ) показывает, что при переходе от Приволжской возвышенности к Клинско-Дмитровской гряде яркость в среднем растет, затем на Клинско-Дмитровской гряде снижается, затем при переходе к Подольскому ополью вновь повышается и, наконец, снижается на Окско-Московской равнине.
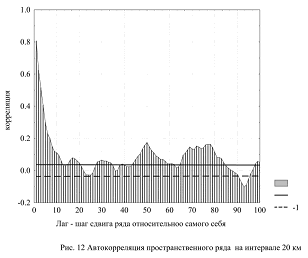
На рис. 12 представлена автокорреляционная функция этого ряда. Именно эта функция показывает, что колебания значений, отражающих состояние поверхности, не являются чисто случайными и в изменении их значений в пространстве существует вполне определенный порядок или закономерность. Во-первых, автокорреляция показывает, что связь между соседними значениями, получаемая при сдвиге ряда относительно самого себя на один шаг, около 0,8. То есть, зная значение в точке i, с достаточно высокой надежностью можно предсказать значение в точке i+1. Во-вторых, по мере увеличения шага сдвига (лага) корреляция падает и становится равной нулю примерно при сдвиге на 21 шаг, то есть 5,2 км на местности. Это означает, что, зная значения фактора в какой-либо точке, ничего нельзя сказать о его значении в точке отстоящей на расстоянии в 5 км. Существование такого медленного затухания связи указывает на наличие в ряду низкочастного тренда, то есть медленных, но устойчивых изменений средних значений при движении с севера на юг. Именно этот тренд и отражен черной жирной линией на рис. 11. Однако корреляция при изменении сдвига не остается постоянной, а испытывает циклические колебания с максимум при сдвиге около 49 и 80 пикселей. Такое изменение автокорреляции указывает на возможное существование в ряду значений квазипериодических колебаний с различным периодом, то есть иерархических уровней.
Полное отображение свойств ряда осуществляется на основе спектрального анализа или разложения ряда функцией Фурье.
Суть дела сводится к тому, что любой временной или пространственный ряд можно описать с помощью L/2 гармоник (L – длина ряда), иначе говоря, синусоидальных и косинусоидальных волн с различными амплитудами. Волновым числом (w) обозначатся номер гармоники, начиная с наибольшей. Периодом колебаний называется интервал, на котором гармоника делает полный цикл (P = L/w). Таким образом, длина ряда отображает самый большой период, а минимальный отображаемый период равен 2. Частота колебаний f = 1/P. Максимальная частота колебаний равна 0,5 и называется частотой Найквиста. В результате спектрального анализа рассчитываются дисперсии для каждой гармоники. Если на какую-то гармонику приходится большая дисперсия, то это означает что именно на этой гармонике или с соответствующей ей
периодичностью действует значительная внешняя или внутренняя сила, порождающая пространственные волны с большой амплитудой. Наличие такого максимума указывает на существование пространственной структуры с линейными размерами, соответствующими периоду колебаний. Такова, коротко, сущность спектрального анализа. Следует отметить, что по спектру ряда можно восстановить все его исходные значения. В результате, вместо запоминания L – чисел достаточно запомнить в два раза меньше – L/2. При этом потери информации не будет.
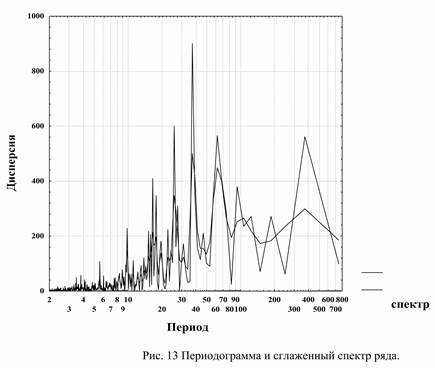
На рис. 13 представлен спектр рассматриваемого ряда. Периодограмма дает прямую оценку дисперсии (или мощности варьирования) на каждый период. Спектр дает оценку по сглаженным значениям. Максимумы варьирования приходятся на периоды 373, 106, 62, 37, 26, 16, 10; 5,6; 3 пикселя, что в принципе индицирует существование 9 иерархических соподчиненных волн, или уровней организации. Периоды соседних уровней в среднем отличаются в два-три раза, что определяет некоторую правильность флюктуаций. В этой правильности скрывается фундаментальное свойство ряда Фурье. Дело в том, что линейной комбинацией гармоник, которые по определению не зависят друг от друга, можно описать любую функцию или любой ряд. Формально каждому из уровней соответствует реальная иерархическая структура в том случае, если она имеет строго синусоидальную форму.
 |
Синусоидальная форма описывает наиболее гармоничную и равновесную пространственную структуру. Если же реальные пространственные структуры не синусоидальны (например, система речных долин, у которых один склон относительно крутой, а другой пологий), то для отображения территориальных структур со сходными линейными размерами потребуется несколько гармоник со строго определенными частотами, кратными целому числу:
fi = foi , i=2,3,4… ,
где f0 – частота гармоники, определяющая собственно иерархический уровень организации. Остальные гармоники с частотами fi – может быть эффектом ортогонального представления ряда разложением Фурье. Однако точно так же такая модель может отражать реальные волны, порождаемые нелинейным характером действия какого-либо фактора. В нелинейных колебаниях, в отличие от линейных, частота колебаний зависит от амплитуды, то есть от мощности воздействия. С ростом амплитуды колебания частота растет и колебания как бы расползаются по нескольким гармоникам. Достигнув некоторого порога мощности, волна «сбрасывается» на более высокую частоту, в силу правила «ухода от резонанса» – в два раза меньшую.
Для того чтобы выявить константную частоту (f0) гармоники, определяемой действием одного фактора, можно рассчитать новый спектр, от уже определенного спектра ряда. Если нет закономерной повторяемости гармоник, различающихся на целое число, то в исходном спектре нет автокорреляции и выраженных гармоник. В этом случае можно говорить, что между выделенными гармониками нет функциональной связи, и каждая из них связана с действием возможно собственного фактора.
Прежде чем перейти к описанному выше разделу анализа колебаний, необходимо рассмотреть содержательную сторону понятия «фрактал» и методы измерения фрактальной размерности. Слово «фрактал» означает «разрыв» и указывает на то, что процесс, подпадающий под понятие «фрактальность», будучи непрерывным, содержит в себе разрывы, то есть области, в которых значения имеют резкий скачок, и производная в этих точках устремляется к бесконечности, то есть отсутствует. Классическим примером фрактального процесса является береговая линия любой территории или любая горизонталь топографической карты. Чем крупнее масштаб построения карты, тем больше в горизонтали появляется изгибов. При этом наблюдается интересный эффект: с ростом масштаба площадь острова или площадь поверхности в рамках одной замкнутой горизонтали стремится к некоторой предельной величине, а длина самой горизонтали (береговой линии) стремится к бесконечности. Очевидно, что это происходит в результате того, что в каждом более крупном масштабе выявляются новые «долины», не наблюдаемые в более мелком масштабе. Сама по себе фрактальность, или фрактальная геометрия, есть чисто математическая модель, как и всякая содержательная модель, отражающая некоторые аспекты реальности. Эта модель в общем случае описывает процессы с бифуркациями или скачкообразные переходы системы из одной локальной области равновесия в другую. Эти переходы могут иметь более или менее регулярный или хаотический характер. В рассмотренном выше примере бифуркация происходит в точке фазового перехода из ламинарного движения воды в грунтах в открытую водную поверхность, или турбулентное русловое течение. То, что переход из одной области состояний в другую происходит скачком, достаточно очевидно. Точно так же слияние двух рек есть скачкообразный переход, порождающий бифуркацию. Обычно такого типа процессы, если они связываются с действием одного фактора, порождают самоподобную структуру: части системы подобны по своей геометрии целому или объединяющей их системе. В этом смысле речная сеть – типичный пример самоподобной системы.
Фрактальная размерность системы в отличие от топологической (точка – ноль размерность; линия – размерность 1; плоскость – размерность 2; куб – размерность 3) нецелочисленна.
Она измеряется фактически как оценка параметра самоподобия. Один из основных методов измерения строится на следующем соотношении [Кронвер,2000]:
1. разделим отрезок прямой на N равных частей. Тогда каждую часть можно считать копией всего отрезка, уменьшенной в 1/r раз. Очевидно, что Nr = 1;
2. рассмотрим то же соотношение для плоскости – Nr2 = 1;
3. то же соотношение для объема – Nr3 = 1;
В общем случае соответственно
Nrd = 1.
Соответственно размерность d:
d = log(N)/log(1/r).
Следовательно, чтобы определить размерность, необходимо организовать процедуру, при которой это соотношение оценивается из уравнения регрессии по нескольким разбиениям ряда, для которого оценивается размерность. Эту процедуру можно организовать нескольким способами.
На рис. 14 исходный ряд значений пересекается одной линией (разбивается на две части), тремя линиями (на четыре части), семью линиями (на восемь частей). В данном методе (метод ящиков) подсчитывается число пересечений линиями графиком (Nr при r = 2,4,8).
Соответственно, размерность определяется из уравнения регрессии между log(Nr) и log(r).
В табл. 9 приведены соответствующие значения Nr и r и параметры уравнения регрессии, а на рис. 15, а график этих демонстрирующий эту связь.
Таблица 9
| Уровни r | |||
| N | 125.0000 | 296.0000 | 452.0000 |
| log2N | 6.965784 | 8.209453 | 8.820179 |
| log2r | |||
| D | 0.927197 | ||
| Ошибка D | 0.182715 |
В соответствии с уравнением регрессии по трем уровням оценки фрактальная размерность линии равна 0,927 и с учетом ошибки недостоверно отличается от целочисленной для линии (1).
Второй способ оценки строится на основе сравнения общей длины линии Lr при изменении масштаба ее представления r. Объект оценки, как и во всех случаях, остается тот же (табл. 10) и D = log(Lr)/log(r). На рис. 16 приведено сравнение длин линий при шаге в 250 м и при шаге r = 16 , 4000 м.
В табл. 10 приведены значения длин линий при различных масштабах отображения трансекта и оценка фрактальной размерности.
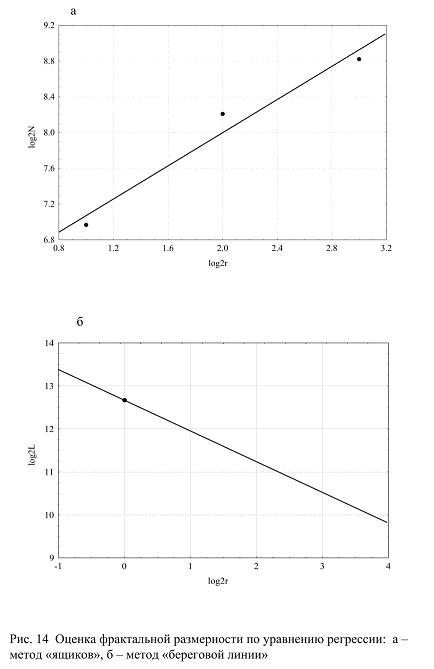
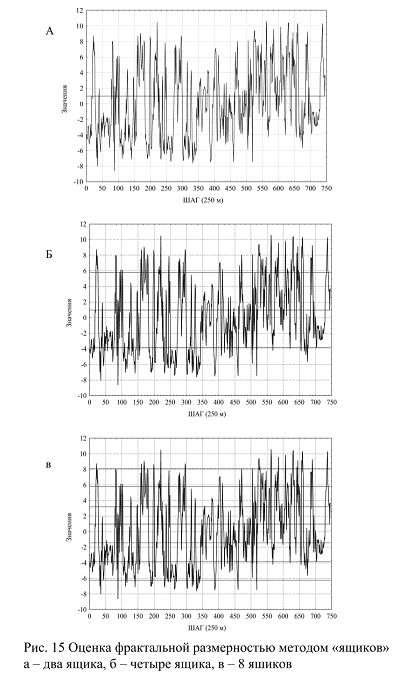
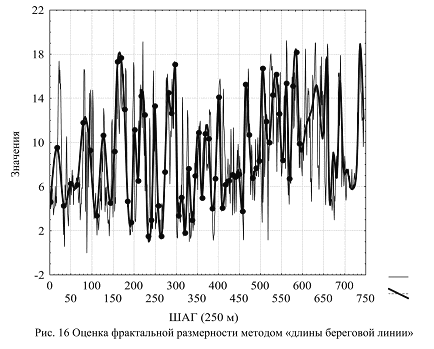
Таблица 10
Расчет фрактальной размерности по модели «изменение масштаба– изменение длины береговой линии»
| Масштаб r | |||||
| L | 6517,51063 | 3306,24844 | 3067,73791 | 1560,53285 | 796,73285 |
| log2N | 12,670105 | 11,690979 | 11,582960 | 10,607823 | 9,637952 |
| log2r | |||||
| D | 0,71475 | ||||
| Ошибка D | 0,08636 |
В этом варианте оценки размерность достоверно отличается от целочисленной (1) и недостоверно от первой оценки 0,93. Различия в оценках в данном случае есть результат лишь различной точности измерения фрактальной размерности.
Более мощным средством является оценка размерности на основе спектральной плотности. Логарифм спектральной плотности (Sp) есть логарифм квадрата среднеквадратического отклонения, то есть амплитуды, поставленной в соответствие конкретной гармоники. Каждая гармоника (w) есть не что иное, как определенный масштаб рассмотрения колебаний (аналог r ), а дисперсия, приходящаяся на соответствующую гармонику, есть аналог квадрата длины линии.
В соответствии с этим
Log(Sp) = a + blog(w) или
log(Sp) = a + blog(1/P).
Так как в данном случае оценка соответствует плоскости, то
D = (5-b)/2.
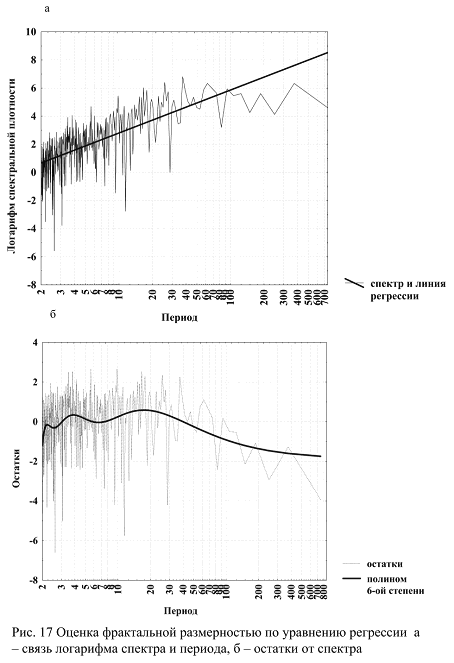
Рассмотрим с этих позиций периодограмму, представленную на рис. 12 в логарифмической форме (рис. 17а). В табл. 11 приведены параметры уравнения регрессии.
Таблица 11
Оценка фрактальной размерности по уравнению регрессии «логарифм спектра – логарифм частоты». Коэффициент корреляции R = 0.66647. Описанное варьирование: 44.418%
| Константа | b | Фрактальная размерность D=(5-b)/2 | |
| Оценка | -0,25127 | -1,3268 | 1,8366 |
| Ошибка | 0,14963 | 0,0771 | 0,0385 |
| t-критерий | -1,67927 | -17,2187 | |
| p-уровень | 0,09394 | 0,0000 |
В данном случае размерность определяется для плоскости, а не для линии, как это было в первых двух методах, и для соизмеримости с первыми оценками из нее нужно вычесть единицу. Таким образом, для линии фрактальная размерность равна 0,8366, что лежит между двумя первыми оценками и отличается от каждой из них статистически недостоверно. Скорее всего, оценку по спектру следует признать наиболее сильной и дающей наиболее точные результаты. Каков смысл оценок фрактальной размерности? Обычно принято выделять три их типа: около 0,5, около 0,1, около 0,9 и 0. Первый тип обычно называют «бурым шумом», и он отражает формы поверхности, порождаемые процессами, связанными с теплопереносом, или диффузией, в основу которых может быть положена модель случайного блуждания. Обычно «бурым шумом» описывается рельеф, целиком определяемый эрозионной системой, близкой к равновесию. Второй тип размерности определяется как «черный шум» и связывается обычно с турбулентными процессами в очень вязкой среде. Обычно такую фрактальную размерность имеет рельеф, сложенный основной мореной или определяемый самоподобной системой разломов. Третий тип размерности называется «розовым шумом» и связывается с турбулетными процессами в среде малой вязкости. Достаточно типична такая размерность для дюнного рельефа. В данном случае фрактальная размерность близка к «розовому шуму», что определяется высокой пространственной контрастностью яркостей, связанной со сменой в пространстве разномасштабных лесных и безлесных территорий. Размерность 0 для линии, 1 для плоскости называют «белым шумом», описывающим чисто случайный стохастический нормальный процесс. Остатки от линии регрессии (рис.17 б) достоверно отличаются от «белого шума» и описываются полиномом шестой степени, который выделяет наиболее статистически достоверные регулярные составляющие пространственных колебаний. В общем, они совпадают с периодическими составляющими, выделенными непосредственно по спектру, однако степени полинома не хватает, чтобы отобразить все отклонения от чисто случайного варьирования.
Формально остатки от уравнения регрессии и полинома должны иметь нормальное распределение и не иметь автокорреляция. Если это условие не выполняется, то в остатках отражаются или тренд, или регулярная составляющая. Если это так, то процесс, отображаемый спектром, не является строго фрактальным, и выделяемые иерархические уровни как наиболее вероятные линейные размеры – достоверны.
Проверка гипотезы о «белом шуме» остатков может осуществляться на основе различных критериев: критерий проверки гипотезы на нормальность распределения, критерий на отсутствие автокорреляций, критерий соответствия спектра экспоненциальному распределению и др.
Не останавливаясь на деталях, отметим, что остатки от полинома 6 степени не являются белым шумом, так что можно полагать, что выделенные выше регулярные составляющие пространственного процесса статистически значимы и реально существуют.
Расчет спектра позволяет определить вторую компоненту разнообразия: разнообразие иерархической организации.
Так как логарифм спектральной плотности отражает варьирование или разнообразие на каждой гармонике, вне зависимости от спектральной плотности на любой другой, то общее иерархическое разнообразие может быть оценено как:
H = SHw = 0.5 Slog(2pe sw) = 0,5(wlog(2pe)+Slog(sw )) – сумма берется по всем гармоникам.
Очевидно, что разнообразие иерархии связано с фрактальной размерностью:
Hw = 0,5(a-log 2pe) –0,5blogw), так как D = (5-b)/2, то b = 5-2D и
Hw = 0,5((a-log 2pe) -(2,5-D)logw.
Удельная энтропия на одну гармонику соответственно есть:
Hw = H/log(w).
Если процесс строго фрактальный и определяется действием только одного фактора, то удельная энтропия есть константа. Таким образом, фрактальную размерность можно рассматривать как оценку разнообразия иерархической организации системы, и чем она больше, тем меньше разнообразие. Следовательно, наиболее сложной организацией, требующей для своего возникновения приложения воздействий очень большой мощности, будут обладать системы, описываемые «розовым шумом». Территории, организация которых отвечает размерности «розового шума», требуют существенно больших хозяйственных усилий для извлечения из них полезной продукции, более сложных стратегий природопользования и при прочих равных условиях более сложны для хозяйственного освоения. В целом же связь разнообразия с фрактальной размерностью имеет фундаментальный характер [Кроновер, 2000; Schroeder,1991].
Рассмотренный пример демонстрирует методы исследования иерархической организации для трансекта со значениями какой либо переменной.
Анализ изображения требует оценки фрактальной размерности для двух мерного случая. Здесь применимы те же методы измерения фрактальной размерности: метод «ящиков», метод масштаба, метод двухмерного спектрального анализа.
Последний метод, хотя и наиболее сложен для расчетов, но дает наиболее полную основу для анализа иерархической организации. В принципе он ничем не отличается от одномерного случая. Двухмерный спектр рассчитывается для всех ортогональных направлений (операцию можно осуществить в программах Surfer 7, Idrisi 32).
На рис. 18 показан логарифм двухмерного спектра в координатах полного периода на все изображение оцениваемого как ±p, рассчитанный для рассматриваемого примера в программе Surfer. Перейти к частотам и волновым числам можно, зная размер изображения (по X – 765 пикселе, по Y = 746). Следовательно, по Х спектр измеряется в диапазоне периодов от 2 до 382, а по Y – от 2 до 373 пикселей.

При такой форме представления, подобласти с противоположными знаками периодов полностью подобны, и верхняя половина рисунка есть зеркальное отображение нижней половины. С другой стороны, отображения в левой и правой половинах несколько различны, что указывает на некоторую общую асимметрию в структурной организации исследуемой территории. В целом же яркость рисунка растет к центру, что прямо указывает на фрактальный характер изображения. На фоне этого общего тренда существует множество локальных максимумов (светлые точки на общем темном фоне), в которых можно заметить некоторые сгущения и разрежевания, но, безусловно, отражающие высокую общую стохастичность иерархической организации территории. Если бы существовали четко выраженные линейные структуры, то в пространстве спектра имелись бы компактные светлые пятна или линии.
D. L. Turcotte [1997] для оценки фрактальной размерности по двухмерному спектру предложил брать его средние значение по радиусам длины wi , соответствующие i – овому волновому числу. Эта операция позволяет свести двухмерное отображение к одномерному. Для отображения асимметрии в организации территории можно рассматривать отдельно средние значения по левой и правой верхним частям изображения спектра. В реализованном пакте программ исследования пространственной организации территории (Fracdim) оценка спектра осуществляется на интервале периодов от 2 до 500 пикселей, что в большинстве случаев достаточно для исследования правил организации конкретной территории [Пузаченко и др., 1999]. При этом следует отметить, что расчет двухмерного спектра для изображений в несколько сотен пикселей требует довольно много машинного времени. Чтобы оценить фрактальную размерность для всего изображения его нужно агрегировать с операцией осреднения, до приемлемых размеров (ширина или высота меньше или равна 500 пикселей).
На рис. 19 показан график двухмерного спектра для изображения в диапазоне 2 – 500 пикселей. Как следует из графика, наклон линии регрессии достоверно изменяется в точке, соответствующей периоду 8 пикселей. Резкое изменение наклона линии регрессии и, соответственно, фрактальной размерности формально указывает на смену физической природы факторов, определяющих иерархическую организацию территории в высокочастотной и низкочастотной частях спектра. Таким образом, территориальные структуры с линейными размерами примерно до 2 км и более 2 км связываются с действием существенно различных факторов. В соответствии с существующими знаниями можно полагать, что за территориальные структуры с линейными размерами меньше 2 км определяются строением четвертичных отложений, вклад которых в формирование структуры на более высоких размерных интервалах резко снижается. Таким образом, оценку фрактальной размерности можно провести для всего изображения и для его отдельных частотных интервалов. В случае двухмерного спектра фрактальная размерность оценивается как D = (7 – b)/2. 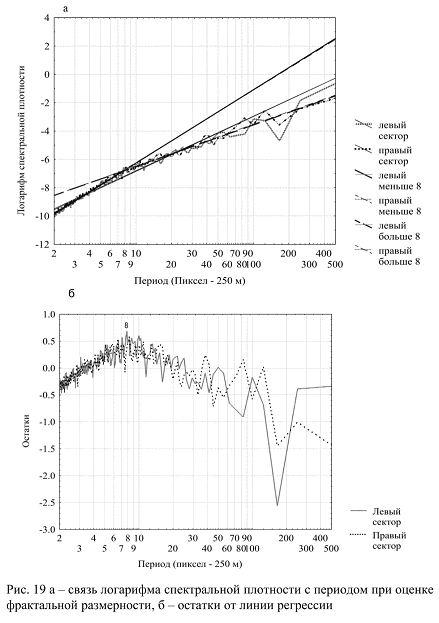
Таблица 12
Дата добавления: 2016-05-25; просмотров: 627;
