Теоретична частина.

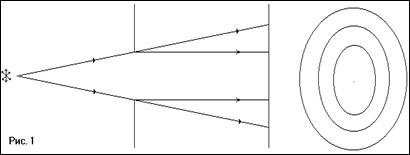Закон прямолінійності поширення світла в оптично – однорідному середовищі, який є основою геометричної оптики, втрачає зміст, якщо розглядати поширення світла після проходження його через вузькі створи або після того як воно зустрічає на своєму шляху дуже малу перешкоду. Так, наприклад, якщо взяти точкове джерело світла і поставити перед ним непрозорий екран з дуже малим створом О, а за ним другий екран Е, то на останньому (див. рис 1.) одержимо від світла , яке пройшло через отвір, освітлений круг, оточений по черзі то темними, то світлими кільцями. Геометричні розміри кілець далеко виходять за межі тих розмірів, які повинні бути за геометричною побудовою на основі закону прямолінійного поширення світла.

Побідні явища спостерігаються і в тому випадку, коли на шляху поширення світла поставити малу перешкоду, наприклад, тонку нитку, то на екрані можна побачити темні і світлі полоси (рис.2). З наведених прикладів випливає, що світло може огинати перешкоди, тобто відхилятись від прямолінійного поширення. Явище огинання світлом непрозорих тіл, що являється відхиленням від прямолінійності поширення в оптично – однорідному середовищі, називається дифракцією світла. Дифракція є результатом хвильової природи світла. Цим явищем можна скористатися для визначення довжини хвилі 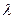видимої частини спектра.

Найбільш цікавий випадок дифракції здійснюється при користуванні дифракційною граткою. Вона являє собою систему близьких паралельних щілин. Частіше для її виготовлення беруть відполіровану скляну пластинку і на її поверхні наносять за допомогою точної ділильної машини ряд паралельних рівновіддалених штрихів. Число штрихів може бути до декількох тисяч на 1 мм. (кількість штрихів на одиницю довжини використовуваної в даній роботі гратки вияснити у викладача). Нанесені на скло штрихи дуже розсіюють світло і виконують роль непрозорих проміжків, між ними залишаються прозорі смужки скла, що відіграють роль щілини.

Світлові хвилі, падають на гратку, огинають штрихи (подряпини) як перешкоди.

Прийнято називати періодом гратки (або постійною гратки d суму ширини прозорої і непрозорої ( а і 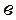) полос (рис 3) :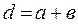

Якщо освітити дифракційну гратку RR пучком когерентних паралельних хвиль (променів), що падають перпендикулярно до поверхні гратки, то спостерігається таке явище :

світло, переходячи через вузькі прозорі полоски гратки RR зазнає дифракції, тобто відхиляється в бік від свого початкового напрямку.

Відхилення променів відбувається під різними кутами 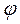. Оскільки кожну щілину гратки можна вважати самостійним джерелом когерентних коливань, то на екрані ММ буде відбуватися накладання численних пучків променів, що приходить в різні точки екрану з певною різницею фаз. Іншими словами, внаслідок явища дифракції ( відхилення променів на різні кути 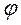) відбувається інтерференція світлових хвиль.

Може бути два випадки:

а) Якщо джерело випромінює світло різних довжин хвиль, то в результаті інтерференції на екрані з’явиться зображення щілин гратки, забарвлене в різні кольори (максимум світла).

б) Якщо джерело дає монохроматичне випромінювання – світло однієї довжини хвилі (таке можна одержати, якщо поставити на шляху променів світловий фільтр), то зображення щілин на екрані (світлові максимуми) будуть забарвлені в один колір – колір фільтра.

Крім кольорових зображень щілин спостерігається ще й темні полоси – місця, де в результаті інтерференції відбулося повне гасіння світлових хвиль (світлові мінімуми).

Вся картина на екрані – сукупність максимумів – носить назву дифракційних спектрів. Умова виникнення максимумів світла визначається співвідношенням: 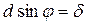, де 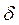- різниця ходу променів.

Якщо 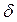кратна цілому числу довжин хвиль, тобто 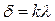, то маємо у відповідній точці екрана максимум світла, і формула набере вигляд :

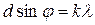( 1 )

де d – період гратки, 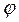- кут дифракції, k – ціле число ( порядок спектра ), тобто номер спектра по відношенню до центральної (нульової) полоси (k = 0, 1, 2, 3 …), 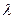- довжина хвилі монохроматичного світла ( світла даного кольору ).

Розв’язуючи рівняння ( 1 ) відносно 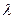, одержимо :

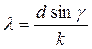( 2 )

Цей вираз є основною формулою для обчислення довжин світлових хвиль за допомогою дифракційної гратки і називається формулою дифракційної гратки .

Схематичний вигляд дифра­кційних спектрів дано на рис. 4.

При k=0 умова максимуму задовольняється для всіх довжин хвиль, тобто при 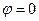спосте­рігається центральна (нульова) світла полоса, яка відповідає невідхиленому пучку променів такого кольору, який колір давало джерело світла.

При k=1 симетрично по обидві боки від центральної полоси одержують дифракційні кольорові лінії, від фіолетової до червоної, які відповідають різним довжинам хвиль, що входять до складу білого світла. Червона частина спектру відхилена більше, ніж фіолетова. Ця група ліній зветься спектром 1 –го порядку.

При k = 2 одержується група ліній подібна – спектр ІІ – го порядку і т. д.

Лінії спектрів високих порядків менш інтенсивні і практично чітко спостерігається спектри не вище ІІІ порядку.

Метод визначення довжини світлової хвилі за допомогою дифракційної гратки полягає в слідую чому. На оптичній лаві, яка включає в себе сильне джерело світла S і конденсатор К, встановіть щілину Щ, об’єктив О і дифракційну гратку RR у вказаній на рис. 5 послідовності.

Дифракційний спектр спостерігають безпо­сере­дньо на екрані ММ. На рис.5 зображені :

R – дифракційна гратка, на яку падає паралельний пучок променів, 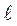- віддаль від дифракційної гратки до екрана ММ, К – віддаль між середніми точками полос одного і того ж спектра (на рис. 5, х – віддаль між серединами полос червоного кольору для спектра і порядку).

Для визначення довжини хвилі 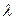за формулою (2) потрібно взнати 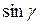. Оскільки кут 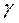- дуже малий 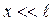то 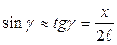( з рис. 5 ).

Підставляючи значення 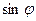у вираз (2), одержимо кінцеву формулу для знаходження довжини хвилі:

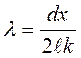(3)

Довжини світлових хвиль вимірюють в нанометрах (1 нм = 10^{-9 м).}