Условие изменения посадки без наклонения судна

Рассмотрим случай, когда посадка судна изменяется в результате приема груза весом Р_гр.

Найдем положение центра массы (тяжести) груза при котором судно не получит наклонения, т.е. новая посадка будет отличаться от первоначальной только на величину дополнительного заглубления DТ.

После приема груза (Р_гр) в воду войдет объем DV (добавочный объем) и, при первоначальных – весе судна D_c и погружном объеме V, уравнение плавучести примет вид

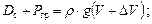
откуда можно получить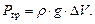

в общем случае при приеме груза сила веса Р_гр и добавочная сила плавучести (r × g × DV) создают момент, вследствие чего судно получает наклонение.

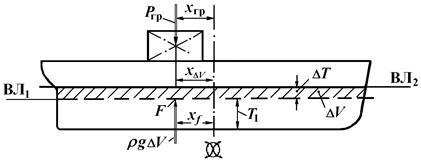
Определим условие приема груза на судно без его наклонения. Рассмотрим, например судно, имеющее начальную посадку прямо и на ровный киль (рис. 2.17).

Рис. 2.17. Изменение посадки при приеме груза

Чтобы при приеме груза не произошло наклонение, вектор веса груза следует расположить на одной вертикали с вектором дополнительной силы плавучести, т.е. должно быть

; .

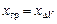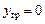(2.5)

Добавочный объем находится между начальной ватерлинией (ВЛ₁, рис. 2.17) и конечной (после приема груза) – ВЛ₂. Площади этих ватерлиний образуют параллельные верхнее и нижнее основания объема DV.

Различают два случая: прием малого груза и прием большого груза.

Прием малого груза. Под малым грузом понимают груз, вызывающий такое изменение осадки, в пределах которого площадь ватерлинии можно считать постоянной. На практике считается, что если масса груза не превышает массу порожнего судна более чем на 20% – для грузовых судов и 10% – для грузопассажирских судов и толкачей, то груз – малый.

Принимается, что при малом грузе вошедший в воду добавочный объем водоизмещения представляет собой вертикальный цилиндр с основанием в виде ватерлинии площадью S₁ = S₂. Центр тяжести объема этого цилиндра находится на вертикали, проходящей через центр тяжести площади ватерлинии (т. F, рис. 2.17) и определяемый абсциссой х_f.

При малом грузе: DV = S × DT и P_гр = r × g × DT × S.

Последняя зависимость позволяет получить формулу 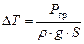, а условие приема груза без наклонения (2.5) запишется в виде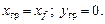

Таким образом, чтобы при приеме малого груза судно не получило наклонение, центр массы груза должен располагаться на одной вертикали с центром тяжести площади ватерлинии.

Прием большого груза. Изменение посадки судна при сохранении q = 0 и некоторого угла дифферента (y₁) можно обеспечить следующим образом.

Для начального состояния судна со шкал углубления считывается осадка на миделе (Т_м) и в оконечностях корпуса . По значениям 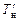и 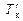, с использованием формулы (2.4) находится осадка судна по носовому перпендикуляру 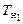и кормовому – 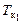. Осадк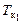и и 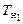позволяют по диаграмме Фирсова (см. рис. 2.14) определить объемное водоизмещение V₁ и абсциссу центра величины 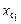для начального состояния судна. Кроме того, по формуле 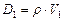(r – плотность воды), определяется массовое водоизмещение.

Для конечного состояния судна (после приема груза) определяется массовое водоизмещение 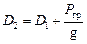, где g – ускорение свободного падения, и, по грузовому размеру (см. рис. 2.10) или по грузовой шкале (см. рис. 2.11), находится изменение осадки (DТ) в результате увеличения массы судна от D₁ до D₂. Для конечного состояния судна осадка носа будет равна 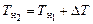, а кормы – 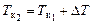. Затем по диаграмме Фирсова, с использованием 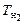и 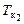, находятся соответствующие значения V₂ и .

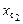В итоге определяется значение абсциссы центра тяжести груза (х_гр) при котором его прием не вызовет наклонение. Это условие выполняется, если центр тяжести груза будет находиться на одной вертикали с центром добавочного объема водоизмещения, т.е. будем иметь: х_гр = х_DV и у_гр = 0.

Исходя из баланса статических моментов погруженных объемов DV, V₁ и V₂ относительно плоскости миделя 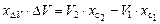и, с учетом того, что DV = V₂ – V₁ нетрудно получить

,

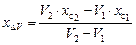где V₂, 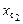– характеристики плавучести судна после приема груза, а V₁, 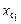– до приема.

Приведенная схема решения задачи о приеме большого груза справедлива и для случая снятия груза. При этом вес груза (Р_гр) следует считать отрицательной величиной и, следовательно, DТ также будет отрицательным.

Если принимается (снимается) несколько грузов, то следует определить их суммарную массу (вес) и положение центра этой совокупности масс.

Задача о приеме большого груза массой Р_г, при условии сохранения прямой посадки (q = 0, y = 0), приближенно решается с использованием показателей по двум ватерлиниям, площади которых образуют верхнее и нижнее основания дополнительного объема DV.

Вначале, при известных значениях осадки Т₁ и массы судна D₁, определяют его массу D₂ = D₁ + P_г, осадку Т₂ и изменение осадки в результате приема груза. Осадка Т₂ и приращение осадки DТ находятся по графику «грузовой размер» (рис. 2.10).

Полученные значения Т₁и Т₂ используются для определения по графику «кривые плавучести» (рис. 2.9) соответствующих значений площади ватерлинии и абсциссы центра тяжести ее площади, т.е. для определения S₁, 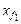, S₂, . последние позволяют приближенно рассчитать абсциссу центра тяжести объема DV по формуле

.

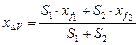(2.6)

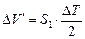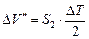Формула (2.6) получена из упрощенного образа объема DV, т.е. предполагается, что этот объем состоит из двух смежных цилиндрических объемов и . Принимается также, что абсцисса центра объема DV¢ равна 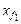, а объема 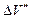– равна .

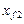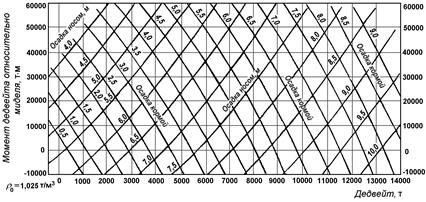
Для решения задач, связанных с изменением посадки судна при q = 0, в эксплуатационной практике широко используется «диаграмма осадок носом и кормой». Такую диаграмму строят в координатных осях: масса судна (D, т) – статический момент массы относительно миделя (М_х, т×м), либо в осях: масса дедвейта судна (Р, т) – статический момент этой массы относительно миделя ( 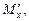т×м). Последний вариант диаграммы представлен на рис. 2.18.

Рис. 2.18. Диаграмма осадок носом и кормой

Диаграмма осадок носом и кормой позволяет решить задачу: по известным значениям массы судна (дедвейта) и статического момента этой массы (расчет – см. табл. 2.1) определить осадку носом и кормой, либо решить обратную задачу. При этом следует учитывать плотность воды, в которой находится судно.