Определение V, xс, zс при посадке судна с креном и дифферентом

Выше рассмотрен случай посадки судна прямо и на ровный киль, когда положение судна определяется одним параметром – осадкой (Т). Зависимостями, представленными на рис. 2.9, 2.10 и 2.11, пользуются для решения задач, как при посадке прямо и на ровный киль, так и при малых значениях дифферента (y < 3°).

Рассмотрим определение основных элементов плавучести при посадке судна с большим дифферентом.

Посадка судна прямо и с дифферентом

В этом случае для выполнения расчетов используется масштаб Бонжана (рис. 2.13).

Такой график представляет собой совокупность кривых, каждая из которых определяет зависимость погруженной площади шпангоута (при q = 0) от его углубления. Масштаб Бонжана строится для 21 теоретического шпангоута; на рис. 2.13, для упрощения, кривые погруженных площадей показаны только для четных шпангоутов (0, 2, 4 и т.д.).

Масштаб Бонжана позволяет вычислять V, х_с, z_c при посадке с любым дифферентом.

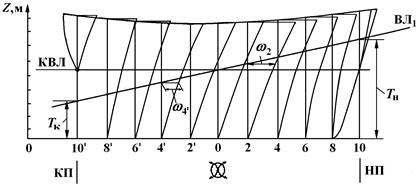
Рис. 2.13. Масштаб Бонжана

Ватерлиния на масштаб Бонжана наносится в виде прямой по заданным осадкам носом Т_н и кормой Т_к, которые откладываются на носовом (НП) и кормовом (КП) перпендикулярах (см. рис. 2.13).

Точки пересечения этой прямой с вертикалями определяют уровень погружения каждого из шпангоутов. Измеряя по горизонтали на уровне этих точек отрезки до соответствующих кривых, получают, с учетом шкалы соответствия линейного размера и площади, погруженные площади шпангоутов ( 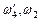на рис. 2.13). Найденные площади являются ординатами строевой по шпангоутам (см. рис. 1.11); с их использованием рассчитывают V (см. табл. 1.3) и x_с (см. формулу (1.29).

Масштаб Бонжана позволяет определить и аппликату центра величины (z_с); такой расчет, ввиду его сложности, в пособии не представлен.

Систематические вычисления на основе масштаба Бонжана выполняют еще в процессе проектирования судна; по их результатам строят диаграммы (рис. 2.14 и 2.15).

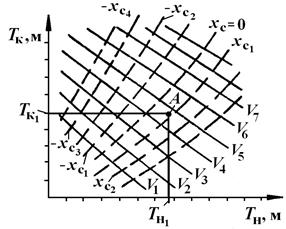
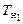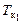На диаграмме Фирсова (см. рис. 2.14) изображают два семейства кривых: постоянного водоизмещения (V) и постоянного значения абсциссы центра величины (x_с). На координатных осях даются значения осадки носом (Т_н) и кормой (Т_к) на перпендикулярах (НП и КП, см. рис. 2.13). Диаграмма Фирсова позволяет по осадкам и без каких-либо дополнительных вычислений определить соответствующие V и x_c (см. рис. 2.14, т.А). по диаграмме аппликат (рис. 2.14) аналогично можно определить значение z_c.

Рис. 2.14. Диаграмма Г.А. Фирсова

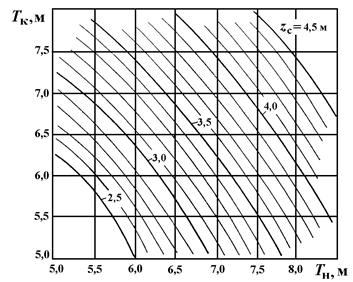
Рис. 2.15. Диаграмма аппликат центра величины

Если, в итоге загрузки (разгрузки) судна, со шкал углубления считаны осадк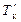и и 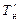, то, затем, по диаграмме Фирсова можно определить соответствующие значения V и x_c, а по диаграмме аппликат (см. рис. 2.15) – значение z_c. Для «входа» в эти диаграммы, исходя из 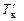и 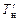выполняется расчет осадки судна по носовому перпендикуляру ( 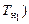и по кормовому ( 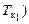с использованием формул

,

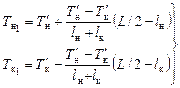(2.4)

где		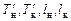–	геометрические показатели представленные на рис. 2.12;
	L	–	длина корпуса между носовым и кормовым перпендикулярами (длина КВЛ).

В эксплуатационной практике нередко решается задача об определении осадки носом и кормой после загрузки или разгрузки судна. Для этого выполняется расчет ожидаемой массы судна D¢ и абсциссы его центра тяжести 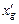по форме табл. 2.1. затем с диаграммы Фирсова (см. рис. 2.14) по точке А, удовлетворяющей условиям 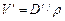и 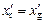, где r – плотность воды, снимаются приближенные значения осадки носом и кормой на перпендикулярах ( ).

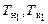Посадка судна с креном и дифферентом

В этом случае для вычисления водоизмещения V и координат центра величины (x_c, z_c) используют интегральные кривые Власова (рис. 2.16).

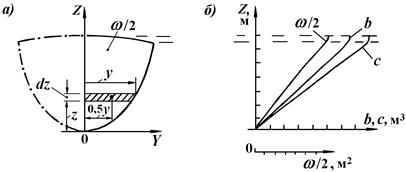
Рис. 2.16. Полушпангоут (а) и интегральные кривые Власова (б)

По каждому шпангоуту, для половины его площади (см. рис. 2.16, а), определяются: площадь погружной части (w/2), а также статический момент этой площади относительно оси 0z (обозначение момента – «b») и статический момент площади относительно оси 0У (обозначение – «с») (см. рис. 2.16, б). Зависимости показателей w/2, b, c от координат У и z шпангоута имеют вид

.

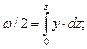
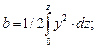
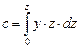Значения показателей w/2, b, c используются для последующего определения, с учетом крена и дифферента, полной погруженной площади шпангоута (w_i), статического момента этой площади относительно оси 0z (обозначение – В_i) и статического момента площади шпангоута относительно оси 0У (c_i).

В итоге, для судна имеющего крен и дифферент, расчет V выполняется с использованием строевой по шпангоутам (ряд w_i) (см. рис. 1.11 и формулу (1.27); для расчета х_с используются w_i и формула (1.29); для расчета у_с используются значения В_i, а расчета z_c – с_i.

Ввиду сложности, расчет V, х_с, z_c на основе кривых Власова здесь не представлен; подробнее об этом см. [ ].

Установлено [3], что влияние угла крена на V, z_c, х_с мало, поэтому диаграммой Фирсова (рис. 2.14) и диаграммой аппликат центра величины, которые рассчитываются при q = 0, можно пользоваться при посадке судна с креном (q < 10°) и дифферентом.