ПЛОЩАДЬ ПРОЕКЦИИ ПЛОСКОЙ ФИГУРЫ
Теорема: Площадь проекции плоского многоугольника на некоторую плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекции.
1 этап: Проектируемая фигура – треугольник АВС, сторона которого АС лежит в плоскости проекции a (параллельна плоскости проекции a).
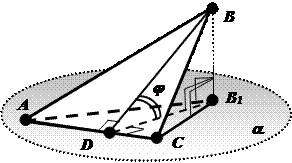Дано:
; 
;
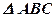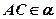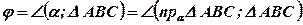
Доказать:
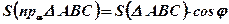
Доказательство:
1. 
; 
;
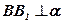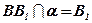2. 
; 
; 
; 
;
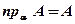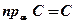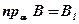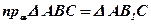3. 
; 
;
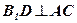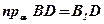4. По теореме о трёх перпендикулярах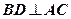 
;
ВD – высота 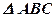; В1D – высота 
;
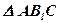5. 
– линейный угол двугранного угла 
;
;
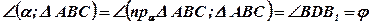6. 
; 
; 
; 
;
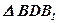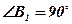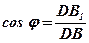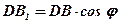7. 
.
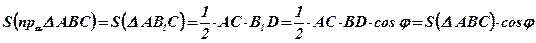2 этап: Проектируемая фигура – треугольник АВС, ни одна из сторон которого не лежит в плоскости проекции a и не параллельна ей.
Дано:
; 
;
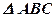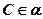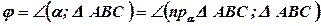
Доказать:
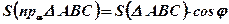
Доказательство:
1. ; ;
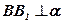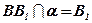2. 
; 
;
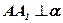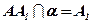3. 
;
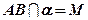4. 
; 
; 
;
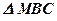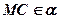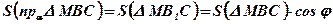(1 этап);
5. 
; ; 
;
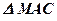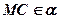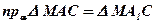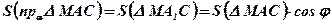(1 этап);
;
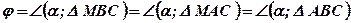6. 
;
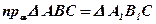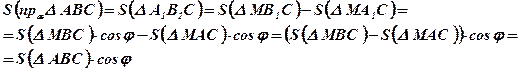
3 этап: Проектируемая фигура – произвольный многоугольник.
Доказательство:
Многоугольник разбивается диагоналями, проведёнными из одной вершины, на конечное число треугольников, для каждого из которых теорема верна. Поэтому теорема будет верна и для суммы площадей всех треугольников, плоскости которых образуют один и тот же угол с плоскостью проекции.
Замечание: Доказанная теорема справедлива для любой плоской фигуры, ограниченной замкнутой кривой.
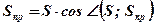
Упражнения:
1. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом 
, если проекция его – правильный треугольник со стороной а.
2. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом , если проекция его – равнобедренный треугольник с боковой стороной 10 см и основанием 12 см.
3. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом , если проекция его – треугольник со сторонами 9, 10 и 17 см.
4. Вычислить площадь трапеции, плоскость которой наклонена к плоскости проекции под углом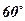 
, если проекция её – равнобедренная трапеция, большее основание которой 44 см, боковая сторона 17 см и диагональ 39 см.
5. Вычислить площадь проекции правильного шестиугольника со стороной 8 см, плоскость которого наклонена к плоскости проекции под углом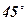 
.
6. Ромб со стороной 12 см и острым углом 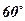образует с данной плоскостью угол . Вычислить площадь проекции ромба на эту плоскость.
7. Ромб со стороной 20 см и диагональю 32 см образует с данной плоскостью угол 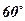. Вычислить площадь проекции ромба на эту плоскость.
8. Проекция навеса на горизонтальную плоскость есть прямоугольник со сторонам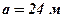и 
и 
. Найти площадь навеса, если боковые грани – равные прямоугольники, наклонённые к горизонтальной плоскости под углом 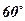, а средняя часть навеса – квадрат, параллельный плоскости проекции.
10. Упражнения по теме «Прямые и плоскости в пространстве»:
1. Стороны треугольника равны 20 см, 65 см, 75 см. Из вершины большего угла треугольника проведён к его плоскости перпендикуляр, равный 60 см. Найти расстояние от концов перпендикуляра до большей стороны треугольника.
2. Из точки, отстоящей от плоскости на расстоянии 
см, проведены две наклонные, образующие с плоскостью углы, равные , а между собой – прямой угол. Найти расстояние между точками пересечения наклонных с плоскостью.
3. Сторона правильного треугольника равна 12 см. Точка М выбрана так, что отрезки, соединяющие точку М со всеми вершинами треугольника, образуют с его плоскостью углы 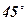. Найти расстояние от точки М до вершин и сторон треугольника.
4. Через сторону квадрата проведена плоскость под углом к диагонали квадрата. Найти углы, под которыми наклонены к плоскости две стороны квадрата.
5. Катет равнобедренного прямоугольного треугольника наклонён к плоскости a, проходящей через гипотенузу, под углом . Доказать, что угол между плоскостью a и плоскостью треугольника равен .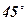
6. Двугранный угол между плоскостями треугольников АВС и DВС равен 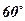. Найти АD, если АВ = АС =5 см, ВС = 6 см, ВD = DС = 
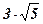см.
Дата добавления: 2016-05-11; просмотров: 4001;