Пример решения задачи №1

Порядок решения задачи в среде пакета Smath Studio

1. Вводим функцию: z(x, y) = sin(x) + cos(y)+0.5. Для вычисления значений функции в заданных точках набираем: z(1.234, 1.543)=. После нажатия клавиши «=» ответ сразу появится на экране. Аналогично поступаем со второй точкой.

2. Для отображения таблицы значений функции одну переменную задаем как константу (например, y1:=π/2), а вторую (x1) – посредством ранжированной переменной с изменением от 0 до 2π с шагом π/5. Таблица появляется на экране после набора «x1=» и «z1=».

3. Построение графика производится выбором на панели инструментов «Функции» пиктограммы «2D» и ввода имени функции. Желательно затем откорректировать вид построенного графика – изменить размер, изменить расположение осей, масштабировать значения переменной и функции для более наглядного представления.

4. Экстремумы (минимальное и максимальное значения) можно найти при помощи функций Min и Max (см. пример).

5. Выводы по пакету Smath Studio: в нем можно быстро и легко записать любую функцию, вычислить ее значения в разных точках и построить график, нетрудно найти точки пересечения функции с осями координат и определить минимальное и максимальное ее значения на отрезке.

На рисунке 2.7 представлен пример решения задачи №1 в среде Smath Studio.

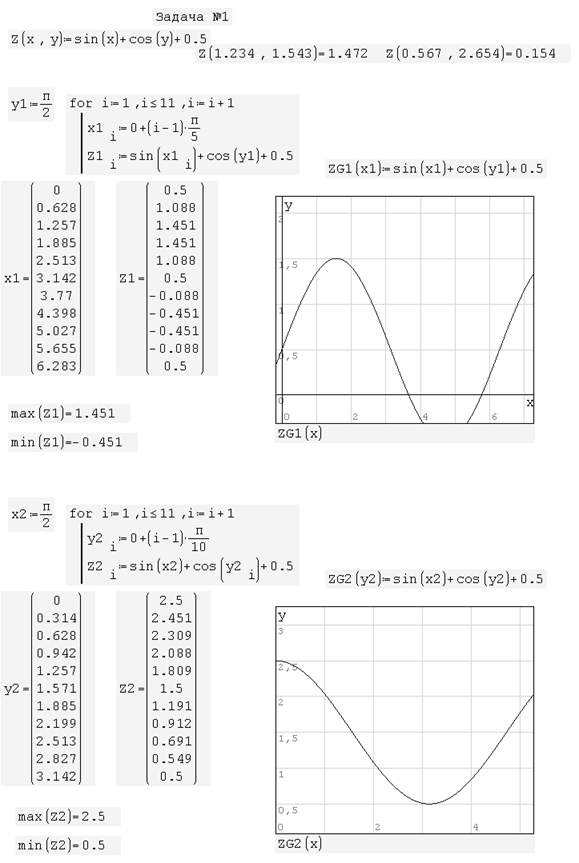
Рисунок 2.7 – Пример решения задачи №1 в среде Smath Studio

Задача № 2

С использованием пакета Smath Studio исследовать функцию вида z = f(x, y) в указанных пределах изменения переменных:

1. Определить максимальное и минимальное значение функции на заданном диапазоне изменения переменных, а также соответствующие значения переменных;

2. Построить и оформить объемный график функции;

3. Сделать выводы по эффективности использования из пакета в том или ином случае.

Список функций для исследования приведен в таблице 2.2.

Таблица 2.2 – Варианты функций к задаче 2

Вариант	Функция	Переменная Х	Переменная У
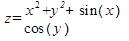
		–30, –15,…, 30	–20, –10,…, 20
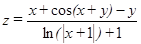
		–45, –30,…, 0	–15, –10,…, 15
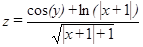
		–20, –15,…, 20	–60, –40,…, 60
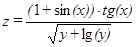
		–80, –40,…, 80	1, 2,…, 7
		–60, –45,…, 30	0, 15,…, 90
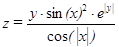
		–45,–30,…,45	0, 0.5,…, 3
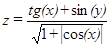
		–60, –30,…, 60	–45, –30,…, 45
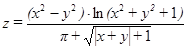
		–20, –15,…, 20	0, 1,…, 6
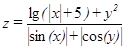
		–60, –30,…, 60	–45, –30,…, 45
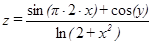
		–30, –20,…, 30	–40, –20,…, 40
		–50, –40,…, 10	1, 3… 10
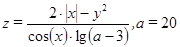
		–25, –20,…, 15	11, 12,…, 17
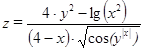
		–70, –50,…, 30	–35, –30,…, 35
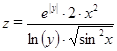
		–35, –30,…, 35	2, 2.5,… 6

Продолжение таблицы 2.2

		5, 10,…, 50	1, 3,…, 10
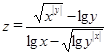
		1, 3,…, 15	2, 4,…, 8
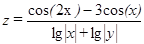
		5, 10,…, 30	11, 12,…, 17
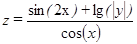
		–10, 0,…, 70	5, 10,…, 45
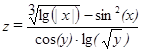
		10, 20,…, 80	2, 2.5,…, 6
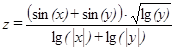
		5, 10,… 45	5, 15,…, 60
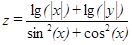
		10, 20,…, 80	2, 4,…, 16
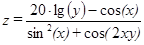
		5, 10,…, 30	11, 12,…, 17
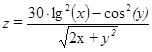
		10, 20,…, 70	5, 10,…, 40
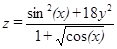
		–40, –30,…, 10	10, 15,…, 65
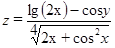
		1, 3,…, 10	0, 10,…, 60
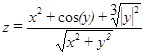
		10, 20,…, 70	1, 2,…, 10
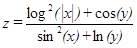
		5, 10,…, 30	2, 4,…, 14
		1, 2,…, 10	10, 15,…, 40