Основы работы в среде пакета Smath Studio
Smath Studio – бесплатный математический пакет с графическим интерфейсом для вычисления математических выражений и построения двумерных и трёхмерных графиков. Поддерживает работу с матрицами, векторами, комплексными числами, дробями и алгебраическими системами. Удобный, графический (как на бумаге) интерфейс и богатые вычислительные возможности программы хорошо сочетаются с достойным количеством настроек и автоматических режимов. В дистрибутив программы также встроен информативный математический справочник. Интерфейс пакета и методика работы с ним во многом схожи с известным и весьма дорогим MathCAD-ом.
Автором проекта является Андрей Ивашов, г. Санкт-Петербург.
Существуют версии программы как для персональных компьютеров под Windows и Linux, так и для КПК, коммуникаторов и смартфонов. Для работы программы требуется Microsoft .NET Framework. Поэтому лучше использовать переносимую (Portable) версию, которую не нужно устанавливать. Подробную информацию о пакете, его установке и ответы на вопросы можно получить на сайте http://ru.smath.info. Интерфейс программы доступен на многих языках и настраивается автоматически.
Верхняя часть рабочего окна Smath Studio содержит меню, правая – панели инструментов (рис. 2.1). В нижней части расположена рабочая область, где вы будете размещать свои документы (формулы, графики, таблицы, текст). Информация вводится в место, указываемое курсором (имеет вид красного крестика). При вводе появляется «интеллектуальная» подсказка, предлагающая ввести функцию либо единицу измерения, наименование которой начинается с введенных символов.
Операции пакета можно выполнять как посредством команд-комбинаций клавиш, так и через меню или же при помощи кнопок на панелях инструментов. Практически все, что нужно для выполнения вычислений находится на панелях инструментов.
В Smath Studio, так же как и в MathCAD все имена переменных и констант регистрозависимы (большие и малые буквы различаются). Кириллицу использовать при этом не рекомендуется. Константу π можно вызвать с панели инструментов «Арифметика». Основание натурального логарифма можно вести просто набрав латинское e.
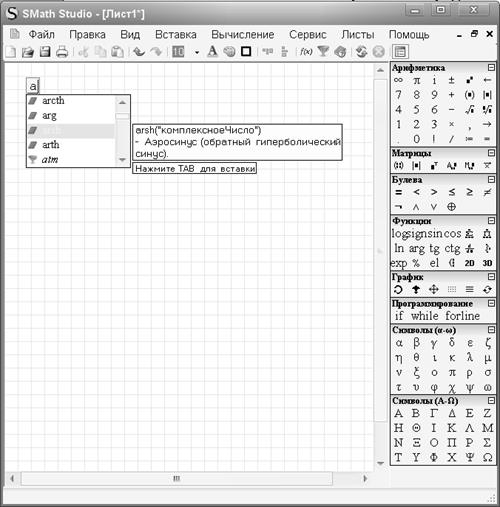
Рисунок 2.1 – Общий вид программы Smath Studio
Для определения переменной следует: ввести ее имя, нажать клавишу двоеточия «:» (находится, где русское «Ж»), по которой помещается знак определения «:=» (можно также найти соответствующую пиктограмму панели инструментов). Т. к. двоеточие находится на верхнем регистре, то нужно удерживать при этом клавишу Shift. После производится запись числа или более сложной конструкции из чисел и предварительно определённых переменных.
Для вывода результата вычислений служит знак «=». При этом должен быть включен режим «Автопересчет» пункта меню «Вычисление». Если не включать этот режим, то для выполнения расчетов следует нажать клавишу «F9».
Ввод должен производиться слева направо или снизу вверх, т. е. формулы должны использовать значения, объявленные выше или левее. Также и вывод результатов может производиться только правее или ниже расчётных формул (рис. 2.2):
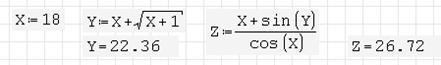
Рисунок 2.2 – Вид расчёта в программе Smath Studio
Пояснения к вычислениям можно ввести при помощи текстовой области. Она может иметь произвольные размеры. Для ее создания используется команда «Вставка\Текстовая область».
Редактирование формул и числовых значений осуществляется следующим образом. Щелкните по объекту, который нужно редактировать. Курсор при этом примет вид черного уголка. Для перемещения курсора на нужный уровень корректировки используйте клавиши со стрелками вправо и влево. Для удаления символов используются те же клавиши Del и BackSpace.
При редактировании часто возникают ошибки связанные с тем, что новый фрагмент формулы вводится как отдельный объект. Поэтому нужно проследить, чтобы обязательно войти в режим редактирования – курсор из красного крестика превращается в черный уголок.
Вычисление нескольких значений переменной либо функции может быть выполнено при помощи элемента массива (рис 2.3). Значения элементов массива вводятся с помощью операции нижнего индекса (клавиша «[» – левая квадратная скобка) а также заполнением вставленного шаблона матрицы по команде «Вставка\Матрица» (комбинация клавиш Ctrl+M).
Ранжированная переменная – это переменная, которой приписан диапазон изменения значений, и каждое использование такой переменной воспринимается как необходимость произвести вычисления по всем её значениям.
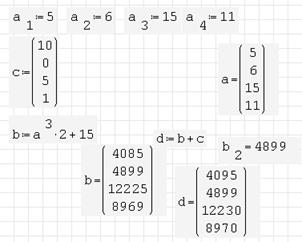
Рисунок 2.3 – Вычисления элементов одномерных массивов
Другим способом определения нескольких значений переменной является его расчет на основе ранжированного индекса. Для этого используется оператор цикла for на панели инструментов «Программирование». Необходимо задать начальное значение некоторой ранжированной переменной, верхнюю границу и её величину приращения (рис 2.4).

Рисунок 2.4 – Использование цикла для изменения индекса
Пакет может использовать как большой набор встроенных функций, так и созданные пользователем дополнительные функции. В этом случае записывается имя функции, затем в скобках перечень используемых при вызове независимых переменных и функций. После символа «:=» записывается сам текст функции. Например:
fv(k):=sin(k)+5.
Для создания области графика курсор устанавливаем в свободную область документа, выбираем панель инструментов «Функции», и в зависимости от требуемого выбираем либо «2D»(двумерный (рис. 2.5)), либо «3D (График поверхности)» (трёхмерный (рис. 2.6)). Действия могут быть выполнены также по комбинациям клавиш: Shift и 2(@) (двумерный), Ctrl и 2(@) (трехмерный).
C помощью панели инструментов «График» можно выполнять вращение, масштабирование и перемещение графика, также задавать отображение точками или линиями, перерисовывать графики заново (в случае такой необходимости). Для построения графиков используется декартова система координат. Вращать можно только трехмерные графики. Можно выполнять масштабирование по осям х и у по отдельности колесиком мыши (при нажатых клавишах Ctrl или Shift соответственно).
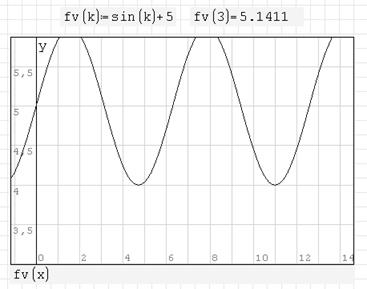
Рисунок 2.5 – Вид области двумерного графика
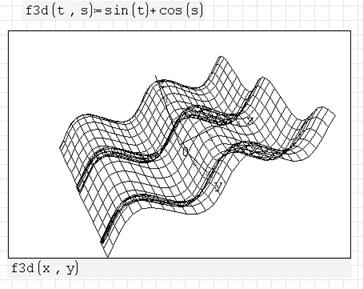
Рисунок 2.6 – Вид области трехмерного графика
При построении двумерного графика в указанном месте документа появляется пустая графическая область с указателем, в который нужно поставить имя рассматриваемой функции. Графики строятся для функций от переменной «x» (2D) или «x» и «y» (3D). Функции могут быть от любых аргументов, но при построении графика должны быть указаны в качестве аргументов именно эти переменные.
Панель инструментов «Программирование» содержит операторы, позволяющие выполнять циклические вычисления (циклы «for» и «while») или задавать функцию условия «if». Линия (line) выполняет функцию операторных скобок. Она по умолчанию содержит два места для последовательных вычислений. Чтобы увеличить количество мест, необходимо выделить линию угловым курсором, затем, зацепив появившуюся квадратную метку курсором, растягивать до необходимого количества мест. Аналогичный способ увеличения количества мест применяется для знака системы.
Панели инструментов «Символы» используются для вставки букв греческого алфавита. Чтобы получить греческую букву при помощи клавиатуры, необходимо ввести латинскую и нажать Ctrl+«G».
Задача № 1
С использованием пакета Smath Studio исследовать функцию вида z = f(x, y):
1. Вычислить значения функции в заданных точках;
2. Привести таблицу значений функций z = f (x, const) и z = f (const, y);
3. Построить графики функций z = f (x, const) и z = f (const, y);
4. Найти минимальное и максимальное значения функций z = f (x, const) и z = f (const, y) на заданном диапазоне.
Примечание: Пункты задания 2 – 4 предполагают любое значение фиксированной переменной из заданного диапазона.
Список функций для исследования приведен в таблице 2.1.
Таблица 2.1 – Функции для исследования в задаче №1
| № | Функция | Диапазон X | Диапазон Y | Точки |
| Z = y sin x + x cos y | 0...2π | 0...2π | A(0.567, 2.654), B(1.234, 1.543) | |
| Z = 2y sin x + cos y | 0...2π | 0...2π | A(1.567, 1.654), B(0.234, 2.543) | |
| z = sin x + 2x cos y | 0...2π | 0...2π | A(1.654, 1.998), B(0.431, 1.012) | |
| z = ey sin x + ex cos y | 0...2π | 0...2π | A(1.456, 1.876), B(1.431, 0.012) | |
| z = ex sin y + ey cos x | 0...2π | 0...2π | A(1.912, 0.432), B(0.612, 1.271) | |
| z = ex – ey | 0...1 | 0...1 | A(0.500, 0.400), B(0.300, 0.500) | |
| z = x2 – y2 | 1...10 | 1...10 | A(5.000, 4.000), B(3.000, 5.000) | |
| z = (x+y)2 – 0.25x2 – y2 | –5...5 | –5...5 | A(–5.000, 4.000), B(3.000, –5.000) |
Продолжение таблицы 2.1
| z = (x+y)3 – x2 – 0.5 y2 | –5...5 | –5...5 | A(–1.000, 1.000), B(0.000, –2.000) | |
| z = (x+y)3 – 2x3 – 0.5y3 | –5...5 | –5...5 | A(–1.345, 1.000), B(0.987, –2.000) | |
| z = (x+y)2 – 3x3 – y3 | –5...5 | –5...5 | A(2.034, –1.000), B(–0.123, 1.000) | |
| z = x2 – 2 x + y2 – 3 y | –5...5 | –5...5 | A(–2.034, 0.035), B(3.109, –2.387) | |
| z = x3 – 2 x + y3 – 2 y | –5...5 | –5...5 | A(–1.259, 2.901), B(–3.111, 1.000) | |
| z = x3 + 2 x + y3 – 2 y | –5...5 | –5...5 | A(2.901, –1.259), B(1.000, –3.111) | |
| z = x3 + 2 x2 – y3 + 2 y | –5...5 | –5...5 | A(–4.123, 1.952), B(4.123, –1.952) | |
| z = x3 + 2 x – y3 + 2 y2 | –5...5 | –5...5 | A(9.613, 1.252), B(–4.123, 9.123) | |
| z = –x3 + 2 x – y3 + 2 y2 | –5...5 | –5...5 | A(9.613, 1.252), B(–4.123, 9.123) | |
| z = –x3 + 2 x + y3 – y2 | –5...5 | –5...5 | A(–9.613, 1.252), B(5.194, –0.923) | |
| z = -x3 – 2 x + 2 y3 – y2 | –5...5 | –5...5 | A(–1.813, 1.812), B(0.194, –0.923) | |
| z = –x3 – 2 x + 2 y3 – y2 | 1...10 | 1...10 | A(0.192, 2.012), B(3.284, 7.777) | |
| z = x4 – 9 x3 + 2 y3 – y2 | 1...10 | 1...10 | A(0.192, 2.012), B(–3.284, 6.666) | |
| z = x4 – 9 x3 – 2 y3 – y | 1...10 | –5...5 | A(5.106, –3.123), B(9.109, –2.222) | |
| z = –x4 + 9 x3 – 2 y3 – y | 0...1 | 0...1 | A(0.500, –0.500), B(–0.500, 1.000) | |
| z = x3 + x2 – 2 y3 – y2 | 0...1 | 0...1 | A(0.500, –0.500), B(–0.500, 1.000) | |
| z = x3 + x2 – x + y2 – y | 0...1 | 0...1 | A(0.666, –0.666), B(–0.666, 0.666) | |
| z = e sin x – e cos y | 0...1 | 0...1 | A(0.901, 0.932), B(0.001, 0.996) | |
| z = y sin x – x cos y | 0...1 | 0...1 | A(0.100, 0.100), B(0.555, 0.666) | |
| z = ln x – e y | 1...10 | 0...1 | A(1.000, 5.000), B(5.000, 1.000) |
Дата добавления: 2016-05-11; просмотров: 7192;
