Структурная схема уравновешивающего преобразования. Аддитивная и мультипликативная погрешности.

Особенность схемы состоит в том, что выходная величина 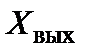, как показано на рис. 5.33, подвергается обратному преобразованию в величину 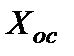, однородную с входной величиной 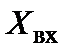и уравновешивающей ее, в результате чего на вход цепи прямого преоразования поступает только небольшая часть входной величины 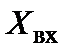. Другими словами, используется отрицательная обратная связь и уравновешивание производится автоматически.

Возможны два режима работы: режим неполного уравновешивания и режим полного уравновешивания. Рассмотрим сначала первый из них.

Прежде всего получим для схемы уравнение преобразования 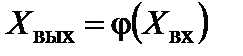. Для этого запишем уравнение связи между сигналами в различных участках схемы. Будем считать справедливыми те же упрощающие предположения в отношении линейности звеньев, которые были приняты при анализе схемы прямого преобразования. Можно записать:

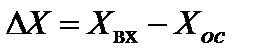(5.69)

уравнение цепи прямого преобразования:

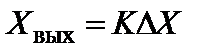(5.70)

уравнение цепи обратного преобразования:

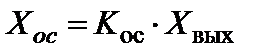(5.71)

Искомое уравнение измерительной схемы будем искать в виде:

(5.72)

где 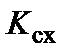- коэффициент преобразования измерительной схемы.

Выразив 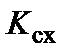из (5.12) и подставляя 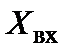, , 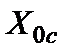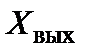из (5.69), (5.70), (5.71), получим

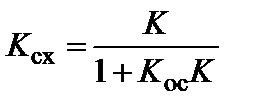(5.73)

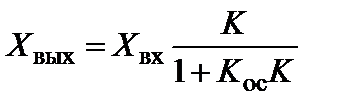(5.74)

Таким образом, выходной сигнал пропорционален входному и зависит от коэффициентов преобразования как цепей прямого, так и обратного преобразования.

Можно видеть, что при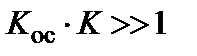

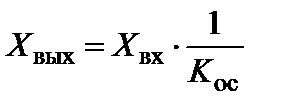(5.75)

то есть цепь прямого преобразования слабо влияет на работу схемы. Для достижения высокой чувствительности следует уменьшить 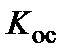, а для выполнения условия 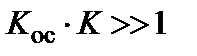следует увеличить К.

Определим мультипликативную погрешность, обусловленную нестабильностями K и 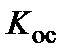. Определим относительную погрешность как погрешность косвенного измерения:

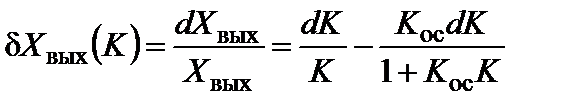(5.76)

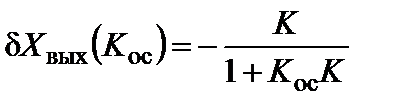(5.77)

так как 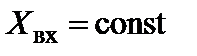. Суммируя (5.16) и (5.17) и переходя к конечным приращениям, получаем:

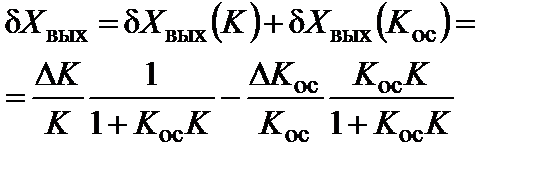(5.78)

Относительная мультипликативная погрешность состоит из суммы двух членов, один из которых пропорционален суммарной погрешности всех преобразователей цепи прямого преобразования, а другой - суммарной погрешности цепи обратной связи. При 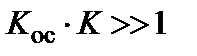погрешность из-за нестабильности K уменьшается в 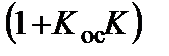раз. Погрешность, обусловленная нестабильностью цепи обратной связи, почти полностью входит в суммарную погрешность. Следовательно, в прямой цепи можно использовать менее стабильные преобразователи, например, усилители, если будет выполнено условие 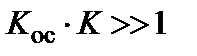. В цепи обратной связи необходимо использовать преобразователи с высокой стабильностью, например, пассивные делители и т. п.

Оценим теперь аддитивную погрешность, обусловленную дрейфом нуля, наводками, помехами, порогом чувствительности звеньев. Введем в структурную схему дополнительные сигналы 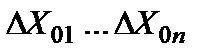, 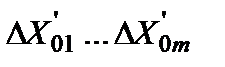. Приведем эти сигналы ко входу схемы. Тогда аддитивная абсолютная погрешность выразится в виде:

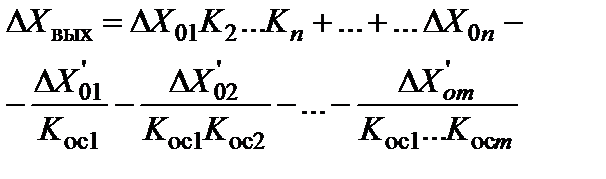(5.79)

Можно видеть, что аддитивная погрешность не зависит от глубины обратной связи и не может быть уменьшена по абсолютной величине введением уравновешивающего преобразования. При увеличении глубины обратной связи будет уменьшаться чувствительность и соответственно возрастать верхний допускаемый предел входной величины.