Структурная схема прямого преобразования. Аддитивная и мультипликативная погрешности.
Отличительная черта схемы прямого преобразования (рис. 5.32) состоит в том, что все преобразования производятся в прямом направлении, то есть предыдущие преобразуются в последующие, а преобразование в обратном направлении отсутствует. Такая схема применяется в приборах с ручным уравновешиванием. При этом уравновешивание (сравнение) производится по последней из преобразованных величин. Так, например, в электронном осциллографе амплитуда измеряемого напряжения, выражаемая в вольтах, преобразуется в конечном счете в длину преображения по оси, выражаемую в сантиметрах. Сравнение амплитуд напряжений в осциллографе производится путем сравнения размеров изображений по оси Y.

|
На схеме рис. 5.32 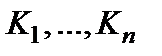 - это преобразователи с коэффициентом преобразования
- это преобразователи с коэффициентом преобразования 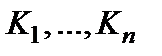 . Здесь
. Здесь 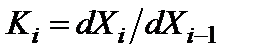 , где
, где 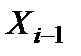 и
и  - входной и выходной сигналы i-го преобразователя.
- входной и выходной сигналы i-го преобразователя.
Входной сигнал 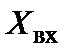 , несущий информацию об измеряемой ФВ, последовательно преобразуется в промежуточные сигналы
, несущий информацию об измеряемой ФВ, последовательно преобразуется в промежуточные сигналы 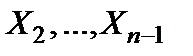 и в выходной сигнал
и в выходной сигнал 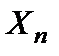 . В РИП сигналы
. В РИП сигналы 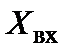 ,
, 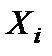 ,
, 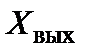 часто представляют собой гармонически изменяющиеся ток или напряжение. Поэтому коэффициенты преобразования
часто представляют собой гармонически изменяющиеся ток или напряжение. Поэтому коэффициенты преобразования 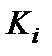 в общем случае выражаются комплексным числом. Для простоты предположим, что информативным параметром сигнала является амплитуда. Тогда
в общем случае выражаются комплексным числом. Для простоты предположим, что информативным параметром сигнала является амплитуда. Тогда 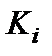 - это вещественные числа. Сделаем также весьма существенное ограничивающее предположение, а именно: коэффициент преобразования не зависит от интенсивности (амплитуды) сигнала, то есть преобразователи считаются линейными относительно выходной и входной ФВ. Очевидно, что в этом случае коэффициент преобразования схемы
- это вещественные числа. Сделаем также весьма существенное ограничивающее предположение, а именно: коэффициент преобразования не зависит от интенсивности (амплитуды) сигнала, то есть преобразователи считаются линейными относительно выходной и входной ФВ. Очевидно, что в этом случае коэффициент преобразования схемы
 , (5.62)
, (5.62)
а уравнение, связывающее 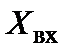
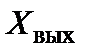 и имеет вид:
и имеет вид:
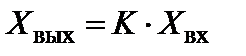 (5.63)
(5.63)
На работу схемы будут оказывать влияние изменения коэффициентов преобразования 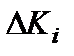 , а также помехи и наводки
, а также помехи и наводки 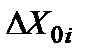 . Оценим величину погрешностей, возникающих из-за наличия
. Оценим величину погрешностей, возникающих из-за наличия 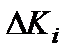 ,
, 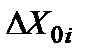 . При этом будем рассматривать суммарную погрешность ∆, то есть содержащую систематическую и случайную составляющие:
. При этом будем рассматривать суммарную погрешность ∆, то есть содержащую систематическую и случайную составляющие:
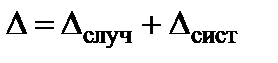 (5.64)
(5.64)
Абсолютная погрешность измерения выходной величины 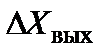 , обусловленная нестабильностью коэффициентов преобразования, может быть определена как погрешность косвенного измерения с учетом выражений 5.62 и 5.63.
, обусловленная нестабильностью коэффициентов преобразования, может быть определена как погрешность косвенного измерения с учетом выражений 5.62 и 5.63.
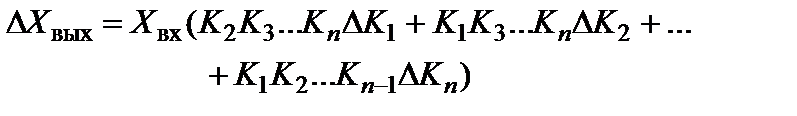 (5.65)
(5.65)
где 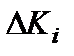 - нестабильность коэффициента преобразования i-го звена.
- нестабильность коэффициента преобразования i-го звена.
Как видно из (5.65), абсолютная погрешность 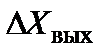 является мультипликативной, то есть пропорциональна, уровню выходного сигнала. Относительная мультипликативная погрешность
является мультипликативной, то есть пропорциональна, уровню выходного сигнала. Относительная мультипликативная погрешность
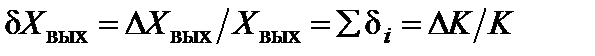 (5.66)
(5.66)
где 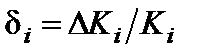 - относительная нестабильность коэффициента преобразования схемы. Результирующая относительная погрешность равна сумме относительных погрешностей преобразователей.
- относительная нестабильность коэффициента преобразования схемы. Результирующая относительная погрешность равна сумме относительных погрешностей преобразователей.
Очевидно, относительные погрешности как приведенные к входной, так и приведенные к выходной величине, равны, если зависимость 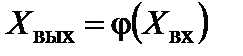 линейна, то есть справедливо (5.63). В общем случае коэффициент преобразования схемы определяется как
линейна, то есть справедливо (5.63). В общем случае коэффициент преобразования схемы определяется как 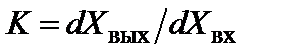 и в случае, если
и в случае, если 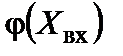 нелинейная зависимость, то
нелинейная зависимость, то  и
и 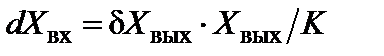 , а
, а
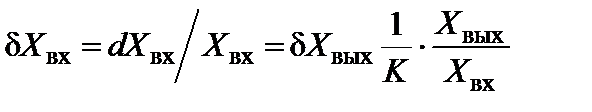 (5.67)
(5.67)
Оценим теперь погрешности, обусловленные помехами и наводками. На схеме рис. 5.32 источники погрешностей показаны в виде дополнительных сигналов 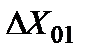 ,
, 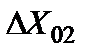 , …,
, …, 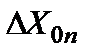 . Результирующее действие этих сигналов эквивалентно действию дополнительного сигнала на выходе:
. Результирующее действие этих сигналов эквивалентно действию дополнительного сигнала на выходе:
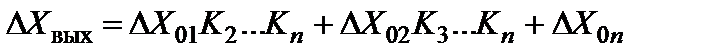 (5.68)
(5.68)
Это аддитивная погрешность, не зависящая от уровня входного сигнала.
Таким образом, как следует из (5.66) и (5.68), в схемах прямого преобразования происходит суммирование погрешностей, вносимых отдельными звеньями. Для достижения высокой точности требуется высокая стабильность всех звеньев.
Дата добавления: 2016-05-11; просмотров: 853;
