Методы деления смешанных затрат на переменные и постоянные компоненты
На практике не всегда можно выделить переменную и постоянную компоненты смешанных затрат, число которых может достигать нескольких десятков. Для этого используются различные методы, суть которых можно раскрыть с помощью графика поведения затрат (рис. 7.5).
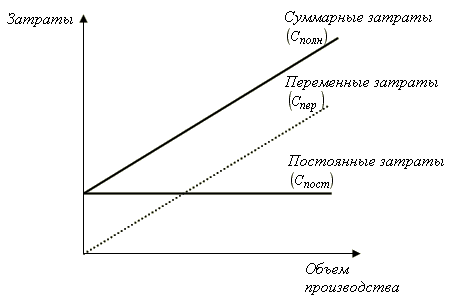
Рис. 7.5. Графическое представление взаимосвязи «затраты ¾ объем»
Общие затраты на производство (Сполн) состоят из двух частей: постоянной (Спост) и переменной (Спер), что отражается уравнением:
Сполн = Спост + Спер . (7.1)
Сумма переменных затрат есть произведение переменных затрат на единицу изделия, т. е. ставки переменных затрат (спер) на объем произведенной продукции в натуральных единицах (Вн.е.):
Спер = спер + Вн.е. (7.2)
Тогда выражение (7.1) можно представить в следующем виде:
Сполн = Спост + спер ´ Вн.е.. (7.3)
На основе конкретных данных строится уравнение общих затрат, которое, аппроксимируя фактические данные, дает представление о зависимости суммарных затрат от объема реализации.
Рассмотрим пример построения уравнения общих затрат и разделения их на постоянную и переменную части с помощью различных методов.
1. Метод высшей и низшей точки объема производства за период (алгебраический метод) предполагает использование следующего алгоритма:
¨ среди данных об объеме производства и затратах за период выбирают максимальное и минимальное значения соответственно объема и затрат;
¨ находят разности в уровнях объема производства и затрат;
¨ определяют ставку переменных затрат на одно изделие путем отнесения разницы в уровнях затрат за период (разность между максимальным и минимальным значениями затрат) к разнице в уровнях объема производства за тот же период;
¨ определяют общую величину переменных затрат на максимальный (минимальный) объем производства путем умножения ставки переменных затрат на соответствующий объем производства;
¨ определяют общую величину постоянных затрат как разность между всеми затратами и переменными затратами;
¨ составляют уравнение совокупных затрат, отражающее зависимость изменений общих затрат от изменения объема производства.
Пример 7.3.В табл. 7.4 приведены исходные данные об объеме производства и затратах по месяцам анализируемого периода.
Таблица 7.4 Данные для анализа затрат с применением метода высшей и низшей точек объема производства за период
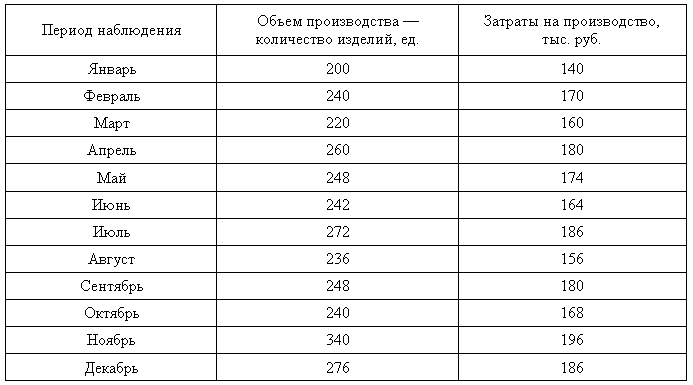
По данным табл. 7.4 видно, что максимальный объем производства за период составляет 340 ед. (в ноябре), минимальный ¾ 200 ед. (в январе). Соответственно максимальные и минимальные затраты на производство равны 196 и 140 тыс. руб. Разность в уровнях объема производства составляет 140 ед. (340 тыс. руб. - 200 тыс. руб.), а в уровнях затрат ¾ 56 тыс. руб. (196 тыс. руб. - 140 тыс. руб.).
Величина переменных затрат на одно изделие составит:
56 000 : 140 = 0,4 тыс. руб./ед.
Общая величина переменных затрат на минимальный объем производства составляет 80 тыс. руб. (0,4 тыс. руб. : ед. ´ 200 ед.), а на максимальный объем ¾ 136 тыс. руб. (0,4 тыс. руб. : ед. ´ 340 ед.). Общая величина постоянных затрат определяется как разность между всеми затратами на максимальный (минимальный) объем производства и переменными затратами. Для нашего примера она составит 60 тыс. руб. (196 тыс. руб. - 136 тыс. руб. или 140 тыс. руб. - 80 тыс. руб.). Уравнение затрат для данного примера в соответствии с выражением (7.3) имеет вид:
Сполн = 60 + 0,4 ´ Вн.е..
Метод высшей и низшей точек прост в применении, но следует отметить его недостатки:
¨ использование только двух значений ¾ наибольшего и наименьшего означает, что результаты могут быть искажены из-за случайных вариаций этих значений;
¨ ссылка на прошлые данные предполагает, что, во-первых, производительность ¾ единственный фактор, влияющий на затраты и, во-вторых, затраты прошлых периодов предопределяют будущие.
2. Метод дисперсии. Более точным является метод дисперсии или разброса, включающий все наблюдаемые точки в стоимостных данных. После изображения точек проводится линия регрессии так, чтобы осталось равное число точек выше и ниже этой линии. Точка пересечения линии регрессии с вертикальной осью покажет сумму постоянных затрат. Используя общие затраты для точки, попавшей на линию регрессии, получают элемент переменных затрат. Далее, разделив эту сумму на уровень деятельности в той же точке, получают ставку переменных затрат.
График дисперсии может оказать большую пользу опытному аналитику. Скачки в поведении затрат, вызванные забастовками, плохой погодой, отключением энергоснабжения, ростом цен в период инфляции, становятся очевидными. Опытный наблюдатель может внести соответствующие поправки (отбросить выскакивающие результаты, оценить надежные данные отдельно, разделить длинный период времени на ряд более коротких интервалов и т. п.). Кроме этого практически любой стоимостный анализ полезно начинать с графического изображения.
Пример 7.4.Необходимо проанализировать смешанные затраты, связанные с доставкой товара. Фактические данные по этим затратам отражены в табл. 7.5.
Таблица 7.5. Данные для проведения анализа затрат с применением метода дисперсии
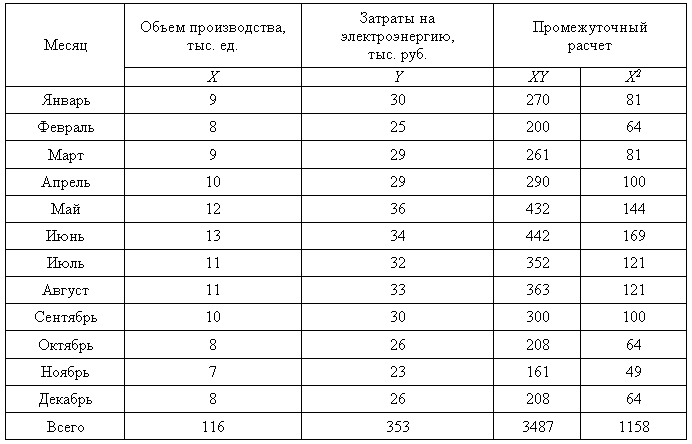
Исходя из графической интерпретации задача заключается в построении по этим данным прямой, изображенной на рис. 7.6.
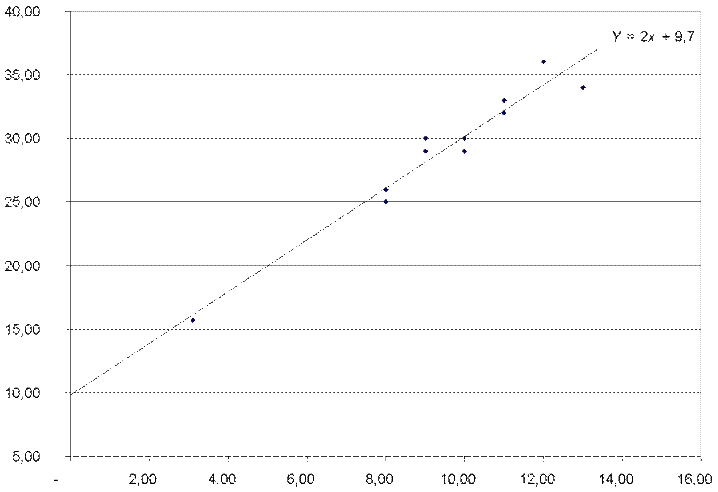 Рис. 7.6. Аппроксимация фактических данных линейной зависимостью
Рис. 7.6. Аппроксимация фактических данных линейной зависимостью
Уравнение затрат в соответствии с выражением (7.3) для данного примера имеет вид:
Сполн = 9,7 + 2 ´ Вн.е..
3. Метод наименьших квадратов. Если при построении графика с использованием метода дисперсии линия вычерчивается визуально, то подбор прямой линии суммарных затрат при использовании метода наименьших квадратов производится с помощью стандартных приемов регрессионного анализа. Он построен на вычислениях, которые основываются на уравнении прямой линии (7.4):
Y = ax + b (7.4)
где Y ¾ зависимая переменная;
a ¾ степень изменчивости (или тангенс угла наклона линии регрессии);
b ¾ постоянный элемент;
x ¾ независимая переменная.
Метод наименьших квадратов используется для нахождения таких a и b, что чтобы полученные из уравнения регрессии значения зависимой переменной Y подходили как можно ближе к ее наблюдаемым значениям. Пусть ошибка:
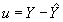 (7.5)
(7.5)
где Y ¾ наблюдаемая величина,
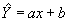 ¾ожидаемая величина.
¾ожидаемая величина.
Метод наименьших квадратов позволяет минимизировать сумму квадратов отклонений наблюдаемой величины от ожидаемой, т. е.:
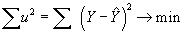 (7.6)
(7.6)
Из основного уравнения (7.6) и множества наблюдений n могут быть получены уравнения регрессии:
∑XY = a∑X2 + b∑X, (7.7)
∑Y = nb + a∑X, (7.8)
где X ¾ объем производства (продаж), натур. ед.;
Y ¾ общие (смешанные) затраты;
a ¾ ставка переменных затрат;
b ¾ постоянные затраты;
n ¾ число наблюдений.
Пример 7.5. Предположим, что предприятие желает разделить свои затраты на переменную и постоянную части. Расходы на электроэнергию (Y) и объем производства (X) представлены в табл. 7.5.
Подставляя эти суммы в уравнения (7.7) и (7.8), получаем:
1158 a + 116 b = 3487; (7.9)
116 a + 12 b = 353. (7.10)
Для решения следует исключить одно из выражений: умножив (7.9) на 12, а (7.10) на 116, следует из (7.9) вычесть (7.10):
13 896 a + 1392 b = 41 844
13 456 a + 1392 b = 40 948
440 a = 896
a = 2,0364
Следовательно, переменная ставка в стоимости электроэнергии составляет 2,0364 тыс. руб. на каждую тысячу выработанных изделий (или 0,0020364 тыс. руб./изделие). Постоянные затраты на электроэнергию могут быть получены подстановкой в любое из уравнений: (7.9) или (7.10):
116 a + 12 b = 353
116 ´ 2,0364 + 12 ´ b = 353
12 b = 353 - 236,2224
12 b = 116,7776
b = 9,7315
Таким образом, постоянные затраты на электроэнергию составляют 9731,5 руб. в месяц, ставка переменных затрат составляет 2036,4 руб. на 1000 выработанных изделий. Уравнение затрат в соответствии с выражением (7.3) для данного примера имеет вид:
Сполн. = 9,7315 + 2,0364 ´ Вн.е.
Формула затрат может быть использована для целей планирования. Предположим, что в течение следующего месяца может быть выработано 10 500 изделий. При таком уровне деятельности затраты на электроэнергию составят, тыс. руб.:
Сполн. = Спост + спер ´ Вн.е.= 9,7315 + 2,0364 ´ 10,5 = 31,1137 тыс. руб.
4. Альтернативный метод. Рассмотрим подход, являющийся альтернативой методу наименьших квадратов. Предположим, что предприятие желает определить формулу затрат на содержание и эксплуатацию оборудования. Предварительный анализ позволил выявить, что переменная часть затрат зависит от количества отработанных машино-часов. Необходимо получить формулу затрат на основе данных первого полугодия планируемого периода альтернативным методом (табл. 7.6).
Таблица 7.6
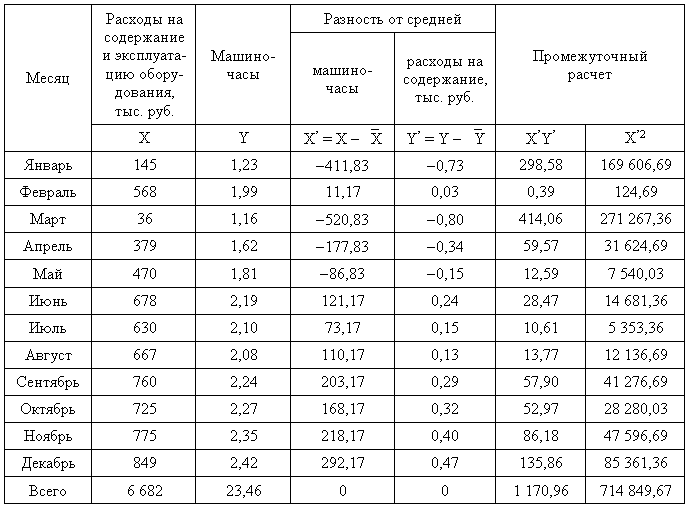
Определяются средние величины:
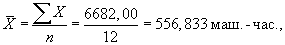 (7.11)
(7.11)
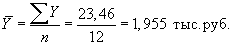 (7.12)
(7.12)
Ставка переменных затрат составляет:
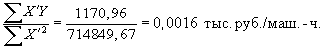
Общие постоянные затраты определяются из уравнения:
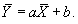 (7.13)
(7.13)
Для данного примера:
0,0016 тыс. руб./маш-ч. ´ 556,833 маш.-ч. + b = 1,955 тыс. руб.;
b = 1,955 - 0,912 = 1,043 тыс. руб. в месяц.
Уравнение затрат в соответствии с выражением (7.3) для данного примера имеет вид:
Сполн. = 1,043 + 0,0016 ´ Вн.е..
График совокупных затрат представлен на рис. 7.7.
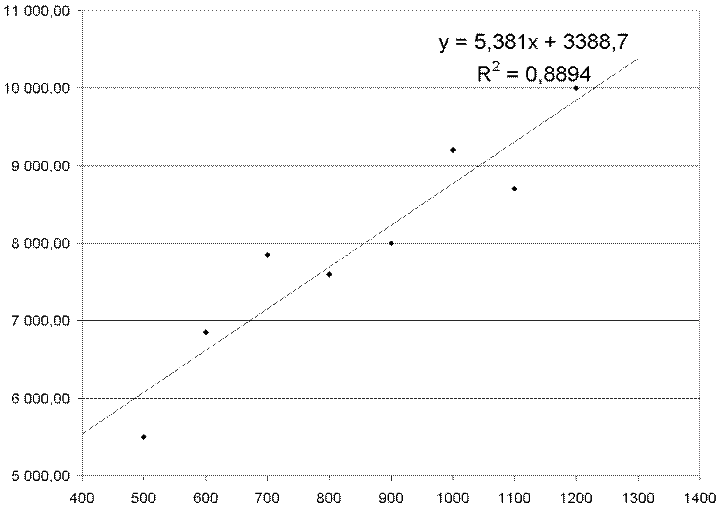
Рис. 7.7. График совокупных затрат
Во всех вычислениях принимался один независимый фактор ¾ производительность (объем производства или реализации, часы прямого труда, машино-часы, выручка от продаж). Но зависимость от объема производства и продаж хорошо просматривается не для всех видов затрат, т. е. не всегда имеет место сильная корреляция конкретного вида затрат от объема производства (продаж). Рекомендуется использовать дополнительные факторы:
¨ объем производства в натуральном выражении;
¨ объем продаж в денежном выражении;
¨ прямые трудовые затраты;
¨ время работы технологического оборудования;
¨ расход электрической энергии и т. д.
Дата добавления: 2017-02-04; просмотров: 5082;
