Статистическое распределение выборки
Пусть изучается некоторая случайная величина  . С этой целью над случайной величиной производится ряд независимых опытов (наблюдений). В каждом из этих опытов величина
. С этой целью над случайной величиной производится ряд независимых опытов (наблюдений). В каждом из этих опытов величина  принимает то или иное значение.
принимает то или иное значение.
Пусть она приняла 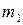 раз значение
раз значение 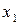 ,
, 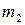 раз – значение
раз – значение 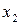 , … ,
, … ,  раз - значение
раз - значение 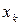 . При этом
. При этом 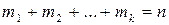 - объем выборки. Значения
- объем выборки. Значения 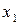 ,
, 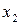 , … ,
, … , 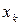 называются вариантами случайной величины
называются вариантами случайной величины  , а изменение этих значений варьированием.
, а изменение этих значений варьированием.
Расположение выборочных наблюдаемых значений случайной величины (признака) в порядке неубывания называется ранжированием статистических данных.
Полученная таким образом последовательность 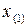 ,
, 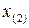 , … ,
, … , 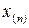 значений случайной величины
значений случайной величины  (где
(где 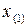
 … £
… £ 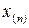 и
и 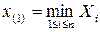 , … ,
, … , 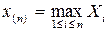 ) называется вариационным рядом.
) называется вариационным рядом.
Числа 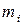 , показывающие сколько раз встречаются варианты
, показывающие сколько раз встречаются варианты 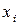 в ряде наблюдений, называются частотами, а отношение их к объему выборки – частостями или относительными частостями (обозначают
в ряде наблюдений, называются частотами, а отношение их к объему выборки – частостями или относительными частостями (обозначают 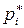 или
или 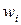 ), то есть
), то есть
 , где
, где 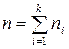 .
.
Перечень вариантов и соответствующих им частот или частостей называется статистическим распределением ряда или статистическим рядом.
Различают дискретные и непрерывные статистические ряды.
Дискретным статистическим рядом называется ранжированная совокупность вариант 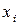 с соответствующими им частотами. Записывается дискретный ряд в виде таблицы. Первая строка содержит варианты, а вторая их частоты или частости.
с соответствующими им частотами. Записывается дискретный ряд в виде таблицы. Первая строка содержит варианты, а вторая их частоты или частости.
Пример 2. В результате тестирования (см. пример 1) группа абитуриентов набрала баллы: 5, 3, 0, 1, 4, 2, 5, 4, 1, 5. Записать полученную выборку в виде статистического ряда.
Решение.
Случайная величина  - число набранных баллов является дискретной случайной величиной.
- число набранных баллов является дискретной случайной величиной.
Вначале составим ранжированный вариационный ряд 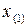 ,
, 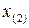 , … ,
, … , 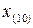 , то есть расположим числа (баллы) в порядке неубывания их величин:
, то есть расположим числа (баллы) в порядке неубывания их величин:
0, 1, 1, 2, 3, 4, 4, 5, 5, 5.
Подсчитав частоту и частость вариантов 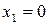 ,
, 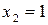 ,
, 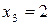 ,
, 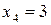 ,
,  ,
,  получим статистическое распределение выборки (так называемый дискретный статистический ряд):
получим статистическое распределение выборки (так называемый дискретный статистический ряд):
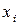
| 
| ||||||
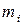
|
или
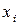
| 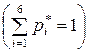 . .
| ||||||
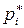
| 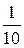
| 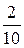
| 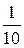
| 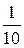
| 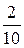
| 
|
В случае, когда число значений признака (случайной величины  ) велико или признак является непрерывным (то есть когда случайная величина
) велико или признак является непрерывным (то есть когда случайная величина  может принять любое значение в некотором интервале), составляют интервальный статистический ряд. В первую строку таблицы статистического распределения вписывают частичные промежутки
может принять любое значение в некотором интервале), составляют интервальный статистический ряд. В первую строку таблицы статистического распределения вписывают частичные промежутки 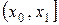 ,
, 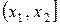 , … ,
, … ,  , которые берут обычно одинаковыми по длине. Для определения величины интервала
, которые берут обычно одинаковыми по длине. Для определения величины интервала 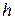 можно использовать формулу Стерджесса:
можно использовать формулу Стерджесса:
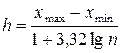 ,
,
где 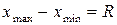 - размах признака, то есть разность между наибольшим и наименьшим значениями признака,
- размах признака, то есть разность между наибольшим и наименьшим значениями признака, 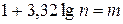 - число интервалов. За начало первого интервала рекомендуется брать величину
- число интервалов. За начало первого интервала рекомендуется брать величину 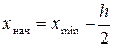 . Во второй строчке статистического ряда вписывают количество наблюдений
. Во второй строчке статистического ряда вписывают количество наблюдений 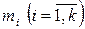 , попавших в каждый интервал.
, попавших в каждый интервал.
Пример 3. Измерили рост (с точностью до 1 см) 30 наудачу отобранных студентов. Результаты измерений таковы:
178, 160, 154, 183, 155, 153, 167, 186, 163, 155, 157, 175, 170, 160, 159,
173, 182, 167, 171, 169, 179, 165, 156, 179, 158, 171, 175, 173, 164, 172.
Построить интервальный статистический ряд.
Решение.
Для удобства проранжируем полученные данные:
153, 154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167,
169, 170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 179, 182, 183, 186.
Очевидно, что рост студентов – непрерывная случайная величина. Для полученной выборки:  ,
, 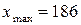 . По формуле Стерджесса, при
. По формуле Стерджесса, при 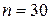 , находим длину частичного интервала:
, находим длину частичного интервала:
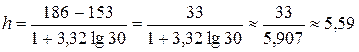 .
.
Примем 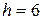 . Тогда
. Тогда 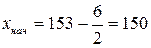 .
.
Число интервалов: 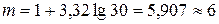 .
.
Исходные данные разбиваем на 6 интервалов: 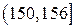 ,
, 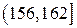 ,
,  ,
, 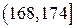 ,
,  ,
, 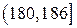 .
.
Подсчитав число студентов ( 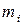 ), попавших в каждый из полученных промежутков получим интервальный статистический ряд:
), попавших в каждый из полученных промежутков получим интервальный статистический ряд:
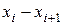
| 150-156 | 156-162 | 162-168 | 168-174 | 174-180 | 180-186 |
Частота 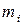
| ||||||
Частость 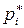
| 0,13 | 0,17 | 0,20 | 0,23 | 0,17 | 0,10 |
Дата добавления: 2016-04-22; просмотров: 4097;
