Метод максимального правдоподобия. Пусть , , , - выборка, полученная в результате проведения независимых наблюдений за случайной величиной

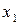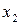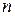Пусть , ,…, - выборка, полученная в результате проведения независимых наблюдений за случайной величиной . И пусть вид закона распределения величины , например вид плотности 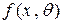, известен, но неизвестен параметр , которым определяется этот закон. Требуется по выборке оценить параметр .

Метод максимального правдоподобия, предложенный Р.Фишером, опирается на использование условий экстремума функции одной или нескольких случайных величин. В качестве такой функции принимают функцию правдоподобия.

Для дискретной случайной величины функция правдоподобия принимает вид

,

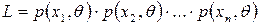где 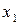, ,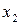…, - варианты выборки;

- параметр, для которого находится оценка;

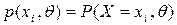- вероятность события 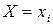, зависящая от параметра .

Для непрерывных случайных величин функция правдоподобия имеет вид:

,

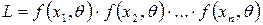где плотность распределения случай ной величины .

Из определения следует, что чем больше значение функции , тем более вероятно (правдоподобнее) появление при фиксированном в результате наблюдений чисел , ,…, .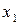

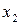За точечную оценку параметра , согласно методу максимального правдоподобия , берут такое его значение 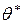, при котором функция правдоподобия достигает максимума.

Так как функции и 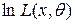достигают максимума при одном и том же значении , то вместо отыскания максимума функции ищут (что проще) максимум функции .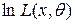

Таким образом, для нахождения оценки максимального правдоподобия надо:

1. решить уравнение правдоподобия

;

2. отобрать то решение, которое обращает функцию 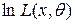в максимум. Удобно использовать вторую производную: если

,

то 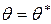- точка максимума (достаточное условие).

Если оценке подлежат несколько параметров 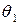, ,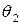…, распределения, то оценки 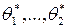определяются решением системы уравнений правдоподобия:

Чаще всего метод максимального правдоподобия используется при биномиальном, пуассоновском и показательном распределениях случайной величины.

В случае биномиального распределения

,

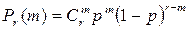где 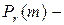вероятность появления ровно 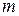раз события 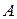(случайной величины) в 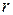испытаниях;

вероятность появления события 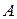в одном испытании.

Величина может рассматриваться как параметр.

Если проводится 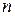опытов по 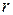испытаний в каждом и фиксируется число появлений события (величины) в каждом испытании 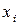, то при подстановке этого значения в формулу биномиального распределения получаем:

.

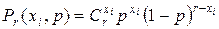Тогда функция правдоподобия примет вид:

.

После логарифмирования и приравнивания к нулю производной от 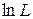получаем выражение для оценки

.

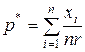Если значения 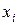встречаются 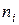раз, то оценка параметра примет вид:

,

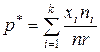где 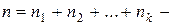число опытов по 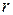испытаний в каждом.