Эмпирическая функция распределения
Эмпирической (статистической) функцией распределения называется функция 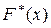 , определяющая для каждого значения
, определяющая для каждого значения 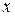 относительную частоту события
относительную частоту события  . Следовательно, по определению:
. Следовательно, по определению:
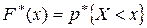 .
.
Для нахождения эмпирической функции распределения удобно 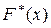 записать в виде:
записать в виде:
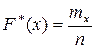 ,
,
где 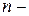 объем выборки,
объем выборки,  число выборочных значений величины
число выборочных значений величины  , меньших
, меньших 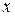 .
.
Эмпирическую функцию распределения можно задать таблично или графически.
Пример 4. Построить функцию 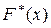 , используя условия и результаты примера 2.
, используя условия и результаты примера 2.
Решение.
Объем выборки по условию примера 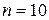 . Наименьшая варианта равна 0, значит
. Наименьшая варианта равна 0, значит  при
при 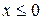 (наблюдений меньше 0 нет). Тогда
(наблюдений меньше 0 нет). Тогда 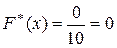 . Если
. Если  , то неравенство
, то неравенство  выполняется для варианты
выполняется для варианты 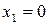 , которая встречается 1 раз (
, которая встречается 1 раз ( 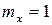 ), поэтому
), поэтому 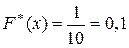 и т.д. Окончательно получаем:
и т.д. Окончательно получаем:
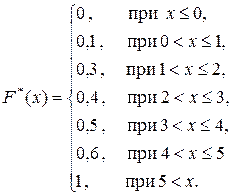
График эмпирической функции распределения приведен на рисунке 1.
 |
Рис. 1. Эмпирическая функция распределения
дискретной случайной величины
В данном примере функция 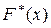 есть выборочная функция распределения дискретной случайной величины и построена она по дискретному статистическому ряду.
есть выборочная функция распределения дискретной случайной величины и построена она по дискретному статистическому ряду.
Если случайная величина непрерывная и ее выборочные значения представлены в виде интервального статистического ряда, то выборочную функцию распределения строят иначе. Рассмотрим построение эмпирической функции распределения для интервального статистического ряда на примере.
Пример 5. Построить функцию 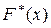 , используя условия и результаты примера 3.
, используя условия и результаты примера 3.
Решение.
Очевидно, что для 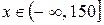
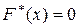 , так как
, так как  .
.
Используя результаты расчетов, представленных в таблице, подсчитаем на концах интервалов значения функции 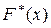 в виде «наращенной относительной частоты»:
в виде «наращенной относительной частоты»:
| Рост | 
| 
| 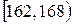
| 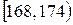
| 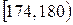
| 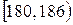
|
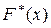
| 0,13 | 0,30 | 0,50 | 0,73 | 0,90 | 1,00 |
Табличные значения не полностью определяют выборочную функцию распределения непрерывной случайной величины, поэтому при графическом изображении такой функции ее доопределяют, соединив точки графика, соответствующие концам интервала, отрезками прямой (рис.2):
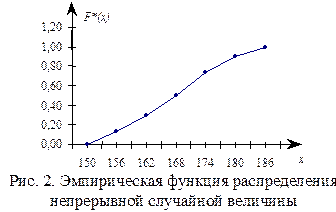
Дата добавления: 2016-04-22; просмотров: 5678;
