Сложение случайных процессов
Пусть требуется найти характеристики случайного процесса Z(t), который является суммой случайных процессов X(t) и Y(t), т.е. Z(t)=X(t)+Y(t), если известны их характеристики: 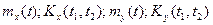 .
.
На основании свойства математического ожидания имеем
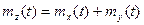 , т.е. при сложении случайных процессов их функции математических ожиданий также складываются.
, т.е. при сложении случайных процессов их функции математических ожиданий также складываются.
Аналогично при сложении любого числа случайных процессов функция математического ожидания суммы этих процессов будет равна сумме функций математических ожиданий этих случайных процессов, т.е.
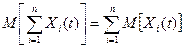 .
.
Найдем корреляционную функцию 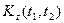 , по определению
, по определению
 .
.
Отсюда
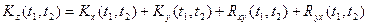 ,
,
где 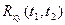 - взаимная корреляционная функция случайных процессов X(t) и Y(t);
- взаимная корреляционная функция случайных процессов X(t) и Y(t);
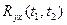 - взаимная корреляционная функция случайных процессов Y(t) и X(t).
- взаимная корреляционная функция случайных процессов Y(t) и X(t).
Взаимной корреляционной функцией случайных процессов X(t) и Y(t) называют неслучайную функцию двух аргументов  , которая для каждой пары аргументов равна корреляционному моменту между соответствующим сечением случайного процесса X(t) и соответствующим сечением случайного процесса Y(t).
, которая для каждой пары аргументов равна корреляционному моменту между соответствующим сечением случайного процесса X(t) и соответствующим сечением случайного процесса Y(t).
Корреляционную функцию  часто называют автокорреляционной функцией.
часто называют автокорреляционной функцией.
При сложении произвольного числа случайных процессов 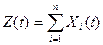 корреляционная функция суммы случайных процессов будет равна сумме автокорреляционных функций плюс сумма взаимных корреляционных функций, т.е.
корреляционная функция суммы случайных процессов будет равна сумме автокорреляционных функций плюс сумма взаимных корреляционных функций, т.е.
 .
.
Если случайные процессы не коррелированны, то 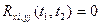 . Тогда
. Тогда
 .
.
Сложение случайного процесса со случайной величиной.Пусть требуется найти характеристики случайного процесса Z(t), который является суммой случайного процесса X(t) и случайной величины Y, т.е. Z(t)=X(t)+Y, если известны их характеристики:  .
.
В случае независимости случайного процесса X(t) и случайной величины Y функцию математического ожидания суммы можно определить по формуле 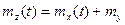 .
.
Дата добавления: 2016-04-19; просмотров: 2231;
