Понятие о марковских случайных процессах

Потоком событийназывают последовательность однородных собы­тий, появляющихся одно за другим в случайные моменты времени. При­меры: поток вызовов на телефонной станции; поток сбоев ЭВМ; поток заявок на проведение расчетов в вычислительном центре и т.п.

Поток событий наглядно изображается рядом точек с абсциссами Q_1, Q₂, ..., Q_n, ... (рис. 6.15) с интервалами между ними: Т₁ = Q₂ - Q_1, T₂ = Q₃ -Q₂, ..., Т_п = Q_n+1 - Q_n. При его вероятностном описании поток событий может быть представлен как последовательность случайных ве­личин:

Q₁; Q₂ = Q₁ + T₁; Q₃ = Q₁ + T₁ + T₂; и т.д.

На рисунке в виде ряда точек изображен не сам поток событий (он случаен), а только одна его конкретная реа­лизация.

Поток событий называется стационар­ным, если его вероятностные характеристики не зависят от выбора начала отсчета или, более конкретно, если вероятность попадания того или другого числа событий на любой интервал времени зависит только от длины этого интервала и не зависит от того, где именно на оси 0-t он расположен.

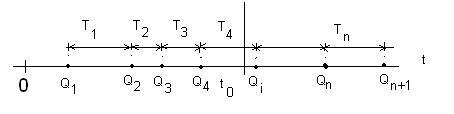
Рисунок 6.15 – Реализация потока событий

Поток событий называется ординарным, если вероятность попадания на элементарный интервал времени двух или более событий пренебре­жимо мала по сравнению с вероятностью попадания одного события.

Рисунок 6.16 – Поток событий как случайный процесс

Ординарный поток событий можно интерпретировать как случайный процесс Х(t) - число событий, появившихся до момента t(рис. 6.16). Случайный процесс Х(t) скачкообразно возрастает на одну единицу в точках Q ,Q₂ ,...,Q _n.

Поток событий называется потоком без последействия, если число собы­тий, попадающих на любой интервал времени , не зависит от того, сколь­ко событий попало на любой другой не пересекающийся с ним интервал. Практически отсутствие последействия в потоке означает, что события, образующие поток, появляются в те или другие моменты времени незави­симо друг от друга.

Поток событий называется простейшим, если он стационарен, ордина­рен и не имеет последействия. Интервал времени T между двумя соседними событиями простейшего потока имеет показательное распределение

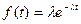(при t>0); (6.21)

где 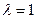/ М [Т] -величина, обратная среднему значению интервала Т.

Ординарный поток событий без последействия называется пуассоновским. Простейший поток является частным случаем стационарного пуассоновского потока. Интенсивностью 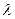потока событий называется среднее число событий, приходящееся на единицу времени. Для стационарного потока 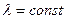; для нестационарного потока она в общем случае зависит от времени: .

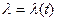Марковские случайные процессы. Случайный процесс называют марковским, если он обладает следующим свойством: для любого момента времени t₀ вероят­ность любого состояния системы в будущем (при t >t₀) зависит только от ее состояния в настоящем (при t =t₀) и не зависит от того, каким обра­зом система пришла в это состояние.

В данной главе будем рассматривать только марковские процессы c дискретными состояниями S_1, S₂, ...,S_n. Такие процессы удобно иллюст­рировать с помощью графа состояний (рис. 5.4), где прямоугольниками (или кружками) обозначены состояния S₁, S₂, … системы S, а стрелками — возможные переходы из состояния в состояние (на графе отме­чаются только непосредственные переходы, а не переходы через другие состояния).

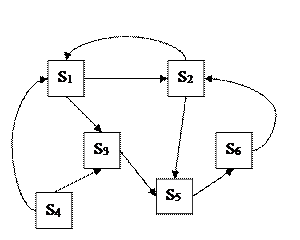
Рисунок 5.4 – Граф состояний случайного процесса

Иногда на графе состояний отмечают не только возможные пере­ходы из состояния в состояние, но и возможные задержки в прежнем состоянии; это изображается стрелкой («петлей»), направленной из данного состояния в него же, но можно обходиться и без этого. Число состояний системы может быть как конечным, так и бесконечным (но счетным).

Марковский случайный процесс с дискретными состояниями и дис­кретным временем обычно называют марковской цепью. Для такого про­цесса моменты t₁, t₂ ..., когда система S может менять свое состояние, удобно рассматривать как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, рассматривать не время t, а номер шага: 1, 2, . . ., k;…. Случайный процесс в этом случае характеризуется последовательностью состояний

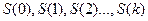, (5.6)

если S(0) — начальное состояние системы (перед первым шагом); S(1) — состояние системы непосредственно после первого шага; ...; S(k) — со­стояние системы непосредственно после k-го шага ....

Событие S_i, , (i= 1,2,...) является случайным событием, поэтому последо­вательность состояний (5.6) можно рассматривать как последователь­ность случайных событий. Начальное состояние S(0) может быть как заданным заранее, так и случайным. О событиях последовательности (5.6) говорят, что они образуют марковскую цепь.

Рассмотрим процесс с n возможными состояниями S_1, S₂, ..., S_n. Если обозначить через Х(t) номер состояния, в котором находится система S в мо­мент t, то процесс описывается целочисленной случай­ной функцией Х(t)>0, возможные значения которой равны 1, 2,...,n. Эта функция совершает скачки от одного целочисленного значения к другому в заданные моменты t₁, t₂, ... (рис. 5.5) и является непрерывной слева, что отмечено точками на рис. 5.5.

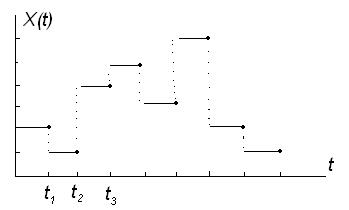
Рисунок 5.5 – График случайного процесса

Рассмотрим одномерный закон распределения случайной функции Х(t). Обозначим через 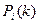вероятность того, что после k-го шага [и до (k+1)-го] система S будет в состоянии S_i (i=1,2,...,n). Веро­ятности р_i(k) называются вероятностями состояний цепи Маркова. Очевидно, для любого k

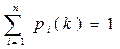. (5.7)

Распределение вероятностей состояний в начале процесса

p₁(0) ,p₂(0),…,p_i(0),…,p_n(0) (5.8)

называется начальным распределением вероятностей марковской цепи. В частности, если начальное состояние S(0) системы S в точности извест­но, например S(0)=S_i, то начальная вероятность P_i (0) = 1, а все остальные равны нулю.

Вероятностью перехода на k-м шаге из состояния S_i в состояние S_j называется условная вероятность того, что система после k-го шага окажется в состоянии S_j при условии, что непосредственно перед этим (после k - 1 шагов) она находилась в состоянии S_i. Вероятности перехода иногда называются также «переходными вероятностями».

Марковская цепь называется однородной, если переходные вероятности не зависят от номера шага, а зависят только от того, из какого состоя­ния и в какое осуществляется переход:

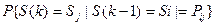(5.9)

Переходные вероятности однородной марковской цепи Р_ij образуют квадратную таблицу (матрицу) размером n * n:

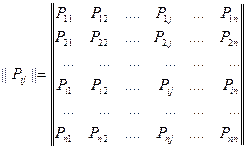(5.10)

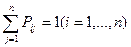. (5.11)

Матрицу, обладающую таким свойством, называют стохастической. Вероятность Р_ij есть не что иное, как вероятность того, что система, при­шедшая к данному шагу в состояние S_j, в нем же и задержится на очеред­ном шаге.

Если для однородной цепи Маркова заданы начальное распределение вероятностей (5.8) и матрица переходных вероятностей (5.10), то вероятности состояний системы могут быть опреде­лены по рекуррентной формуле

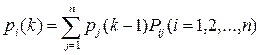(5.12)

Для неоднородной цепи Маркова вероятности перехода в матрице (5.10) и формуле (5.12) зависят от номера шага k.

Для однородной цепи Маркова, если все состояния являются сущест­венными, а число состояний конечно, существует предел определяемый из системы уравнени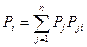й и 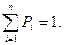Сумма переходных вероятностей в любой строке матрицы равна единице.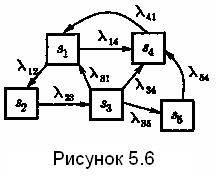

При фактических вычислениях по формуле (5.12) надо в ней учитывать не все состояния S_j, а только те, для которых переходные вероятности отличны от нуля, т.е. те, из которых на графе состояний ведут стрелки в состояние S_i.

Марковский случайный процесс с дискретными состояниями и непрерывным временем иногда называют «непрерывной цепью Маркова». Для такого процесса вероятность перехода из состояния S_i в S_j для любого момента времени равна нулю. Вместо вероятности перехода p_ij рассматривают плотность вероятности перехода 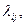которая определяется как предел отношения вероятности перехода из состояния S_i в состояние S_j за малый промежуток времени 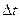, примыкающий к моменту t, к длине этого промежутка, когда она стремится к нулю. Плотность вероятности перехо­да может быть как постоянной ( 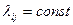), так и зависящей от времени [ 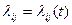]. В первом случае марковский случайный процесс с дискретными состояниями и непрерывным временем называется однородным. Типичный пример такого процесса - случайный процесс Х(t), представ­ляющий собой число появившихся до момента t событий в простейшем потоке ( рис. 5.2).

При рассмотрении случайных процессов с дискретными состояниями и непрерывным временем удобно представлять переходы системы S из состояния в состояние как происходящие под влиянием некоторых по­токов событий. При этом плотности вероятностей перехода получают смысл интенсивностей 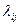соответствующих потоков событий (как только происходит первое событие в потоке с интенсивностью 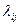, система из со­стояния S_i скачком переходит в Sj). Если все эти потоки пуассоновские, то процесс, протекающий в системе S, будет мар­ковским.

Рассматривая марковские случайные процессы с дискретными со­стояниями и непрерывным временем, удобно пользоваться гра­фом состояний, на котором против каждой стрелки, ведущей из состоя­ния S_{i ,} в S_j проставлена интенсивность 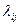потока событий, переводящего систему по данной стрелке (рис.5.6). Такой граф состояний называ­ют размеченным.

Вероятность того, что система S, находящаяся в состоянии S_i, за эле­ментарный промежуток времени ( 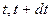) перейдет в состояние S_j (эле­мент вероятности перехода из S_i в S_j), есть вероятность того, что за это время dt появится хотя бы одно событие потока, переводящего систему S из S_i в S_j. С точностью до бесконечно малых высших порядков эта вероятность равна .

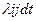Потоком вероятности перехода из состояния Si в Sj называется вели­чина 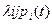(здесь интенсивность 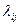может быть как зависящей, так и не­зависящей от времени).

Рассмотрим случай, когда система S имеет конечное число состояний S_1, S₂,..., S_п. Для описания случайного процесса, протекающего в этой системе, применяются вероятности состояний

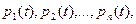(5.13)

где р_i (t) — вероятность того, что система S в момент t находится в состоя­нии S_i:

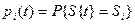. (5.14)

Очевидно, для любого t

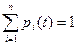. (5.15)

Для нахождения вероятностей (5.13) нужно решить систему диф­ференциальных уравнений (уравнений Колмогорова), имеющих вид

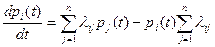(i=1,2,…,n),

или, опуская аргумент t у переменных р_i,

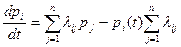(i=1,2,…,n). (5.16)

Напомним, что интенсивности потоков 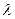_ij могут зависеть от времени .

Уравнения (5.16) удобно составлять, пользуясь размеченным гра­фом состояний системы и следующим мнемоническим правилом: произ­водная вероятности каждого состояния равна сумме всех потоков веро­ятности, переводящих из других состояний в данное, минус сумма всех потоков вероятности, переводящих из данного состояния в другие. Напри­мер, для системы S, размеченный граф состояний которой дан на рис. 10.6, система уравнений Колмогорова имеет вид

(5.17)

Так как для любого t выполняется условие (5.15), можно любую из вероятностей (5.13) выразить через остальные и таким образом уменьшить число уравнений на одно.

Чтобы решить систему дифференциальных уравнений (5.16) для вероятностей состояний р₁(t) p ₂(t), …, p_n(t), нужно задать начальное распределение вероятностей

p₁(0),p₂(0), …,p_i(0), …,p_n(0), (5.18)

сумма которых равна единице.

Если, в частности, в начальный момент t = 0 состояние системы S в точности известно, например, S(0) =S_i , и р_i (0) = 1, то остальные вероятноcти выражения (5.18) равны нулю.

Во многих случаях, когда процесс, протекающий в системе, длится достаточно долго, возникает вопрос о предельном поведении ве­роятностей р_i(t) при 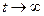. Если все потоки событий, переводящие систему из состояния в состояние, являются простейшими (т.е. стацио­нарными пуассоновскими с постоянными интенсивностями 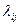), в неко­торых случаях существуют финальные(или предельные) вероятности со­стояний

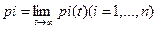, (5.19)

независящие от того, в каком состоянии система S находилась в началь­ный момент. Это означает, что с течением времени в системе S устанавли­вается предельный стационарный режим, в ходе которого она переходит из состояния в состояние, но вероятности состояний уже не меняются. В этом предельном режиме каждая финальная вероятность может быть истолкована как среднее относительное время пребывания системы в дан­ном состоянии.

Систему, в которой существуют финальные вероятности, называют эргодической. Если система S имеет конечное число состояний S₁ , S₂ , . . . , S_n, то для су­ществования финальных вероятностей достаточно, чтобы из любого со­стояния системы можно было (за какое-то число шагов) перейти в любое другое. Если число состояний S₁ , S₂ , . . . , S_n, бесконечно, то это условие перестает быть достаточным, и существование финальных вероятностей зависит не только от графа состояний, но и от интенсивностей .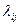

Финальные вероятности состояний (если они существуют) могут быть получены решением системы линейных алгебраических уравнений, они получаются из дифференциальных уравнений Колмогорова, если по­ложить в них левые части (производные) равными нулю. Однако удобнее составлять эти уравнения непосредственно по графу состояний, пользу­ясь мнемоническим правилом: для каждого состояния суммарный выхо­дящий поток вероятности равен суммарному входящему. Например, для системы S, размеченный граф состояний которой дан на р 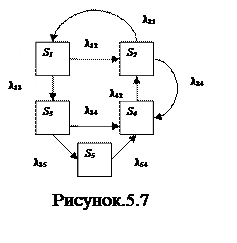ис. 5.7, уравнения для финальных вероятностей состояний имеют вид

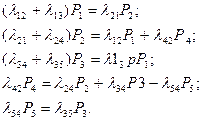(5.20)

Таким образом, получается (для системы S с п состояниями) система n однород­ных линейных алгебраических уравнений с n неизвест­ными р_1, р₂, ..., р_п. Из этой системы можно найти неизвестные р₁ , р₂ , . . . , р_п с точностью до произвольного множителя. Чтобы найти точные значения р₁,..., р_п, к уравнениям добавляют нормировочное условие p₁ + p₂+ …+ p_п =1, пользуясь которым можно выразить любую из ве­роятностей p_i через другие (и соответственно отбросить одно из уравне­ний).

Вопросы для повторения

1 Что называют случайной функцией, случайным процессом, сечением случайного процесса, его реализацией?

2 Как различаются случайные процессы по своей структуре и характеру протекания во времени?

3 Какие законы распределения случайной функции применяют для описания случайной функции?

4 Что представляет собой функция математического ожидания случайной функции, в чем ее геометрический смысл?

5 Что представляет собой функция дисперсии случайной функции, в чем ее геометрический смысл?

6 Что представляет собой корреляционная функция случайного процесса, и что она характеризует?

7 Каковы свойства корреляционной функции случайного процесса?

8 Для чего введено понятие нормированной корреляционной функции?

9 Объясните как по опытным данным получить оценки функций характеристик случайного процесса?

10 В чем отличие взаимной корреляционной функции от автокорреляционной функции?

11 Какой случайный процесс относят к стационарным процессам в узком смысле и в широком?

12 В чем заключается свойство эргодичности стационарного случайного процесса?

13 Что понимают под спектральным разложением стационарного случайного процесса и в чем его необходимость?

14 Какова связь между корреляционной функцией и спектральной плотностью стационарной случайной функции?

15 Что называют простейшим потоком событий?

16 Какой случайный процесс называют марковской цепью? В чем заключается методика расчета ее состояний?

17 Что представляет собой марковский случайный процесс с дискретными состояниями и непрерывным временем?

Упражнения

6.1 Случайная функция 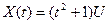, где U – случайная величина, возможные значения которой принадлежат интервалу (0,10). Найти реализации функции X(t) в двух испытаниях, в которых величина U приняла значения: .

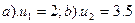6.2 Случайная функция 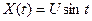, где U – случайная величина. Найти сечения X(t), соответствующие фиксированным значениям аргумента: .

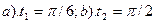6.3 Найти математическое ожидание случайной функции: 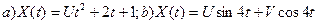, где U и V – случайные величины, причем M(U)=M(V)=1.

6.4 Найти: а) математическое ожидание; б) корреляционную функцию; в) дисперсию случайной функции 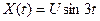, где U – случайная величина, причем M(U)=10, D(U)=0.2.

6.5 Найти нормированную взаимную корреляционную функцию случайных функций X(t)=t*U и Y(t)=(t+1)U, где U – случайная величина, причем дисперсия D(U)=10.