Характеристики случайного процесса

Рассматривая случайный процесс как систему уже трех – четырех случайных величин возникают трудности в аналитическом выражении законов распределения случайного процесса. Поэтому в ряде случаев ограничиваются характеристиками случайного процесса, аналогичными числовым характеристикам случайных величин.

Характеристики случайного процесса в отличие от числовых характеристик случайных величин представляют собой неслучайные функции. Среди них для оценки случайного процесса широко применяются функции математического ожидания и дисперсии случайного процесса, а также корреляционная функция случайного процесса.

Математическим ожиданием случайного процесса X(t) называется неслучайная функция , которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайного процесса

.

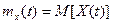Из определения математического ожидания случайного процесса вытекает, что если известна одномерная плотность вероятности 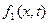, то

. (6.3)

Случайный процесс X(t) всегда можно представить как сумму элементарных случайных функций

, где - элементарная случайная функция.

Тогда

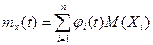. (6.4)

Если задано множество реализаций случайного процесса X(t), то для графического представления математического ожидания проводят ряд сечений и в каждом из них находят соответствующее математическое ожидание (среднее значение), а затем через эти точки проводят кривую (рис. 6.3).

Рисунок 6.3 – График функции математического ожидания

Чем больше проведено сечений, тем точнее будет построена кривая.

Математическое ожидание случайного процесса есть некоторая неслучайная функция, около которой группируются реализации случайного процесса.

Если реализации случайного процесса представляют собой ток или напряжение, то математическое ожидание трактуют как среднее значение тока или напряжения.

Дисперсией случайного процесса X(t) называется неслучайная функция 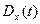, которая при каждом значении аргумента t равна дисперсии соответствующего сечения случайного процесса.

.

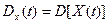Из определения дисперсии случайного процесса вытекает, что если известна одномерная плотность вероятности 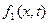, то

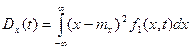или (6.5)

Если случайный процесс представляется в виде , то

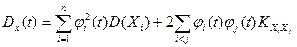. (6.6)

Дисперсия случайного процесса характеризует разброс или рассеивание реализаций относительно функции математического ожидания.

Если реализации случайного процесса представляют собой ток или напряжение, то дисперсию 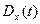трактуют как разность между мощностью всего процесса и мощностью средней составляющей тока или напряжения в данном сечении, т.е.

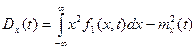. (6.7)

В ряде случаев вместо дисперсии случайного процесса используется среднее квадратичное отклонение случайного процесса

.

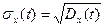Математическое ожидание и дисперсия случайного процесса позволяют выявить вид средней функции, около которой группируются реализации случайного процесса, и оценить их разброс относительно этой функции. Однако внутренняя структура случайного процесса, т.е. характер и степень зависимости (связи) различных сечений процесса между собой, остается при этом неизвестной (рис. 6.4).

Рисунок 6.4 – Реализации случайных процессов X(t) и Y(t)

Для характеристики связи сечений случайного процесса вводится понятие смешанной моментной функции второго порядка - корреляционной функции.

Корреляционной функциейслучайного процесса X(t) называется неслучайная функция , которая при каждой паре значений равна корреляционному моменту соответствующих сечений случайного процесса:

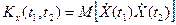, где , .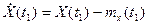

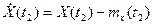Связь (см. рис. 6.4) между сечениями случайного процесса X(t) больше, чем между сечениями случайного процесса Y(t), т.е.

.

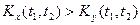Из определения следует, что если задана двумерная плотность вероятности 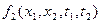случайного процесса X(t), то

, (6.8)

или

. (6.9)

Корреляционная функция представляет собой совокупность корреляционных моментов двух случайных величин 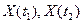в моменты , причем оба момента рассматриваются в любом сочетании всех текущих возможных значений аргумента t случайного процесса. Таким образом, корреляционная функция характеризует статистическую связь между мгновенными значениями в различные моменты времени.

Свойства корреляционной функции.

1) Если 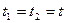, то 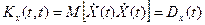. Следовательно, дисперсия случайного процесса является частным случаем корреляционной функции.

2) Корреляционная функция симметрична относительно своих аргументов, т.е. .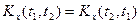

3) Чем больше интервал между , тем корреляционная функция меньше.

4) Геометрически корреляционная функция представляет собой поверхность (рис.6.5).

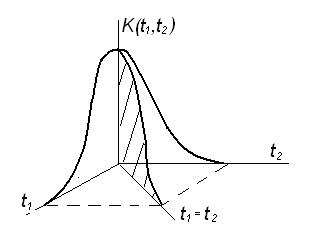
Рисунок 6.5 – График корреляционной функции для часто встречающихся случайных процессов

Во многих случаях особенно при сравнении различных случайных процессов вместо корреляционной функции рассматривают нормированную корреляционную функцию 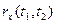, которая определяется как отношение корреляционной функции к произведению функций средне квадратичных отклонений, т.е.

.

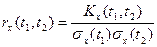Нормированная корреляционная функция 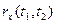, также как и коэффициент корреляции двух случайных величин изменяется от -1 до +1, но не является постоянной, а зависит от аргументов .