Закон распределения случайного процесса

Под законом распределения случайного процесса понимают всякое соотношение, устанавливающее связь между реализацией случайного процесса и вероятностью ее появления.

Пусть нас интересует реализация случайного процесса x(t), проходящая через точки (таблица 6.1).

Таблица 6.1

Функция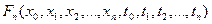называетсяn – мерной функцией распределения вероятностей случайного процесса и определяется как вероятность того, что случайный процесс X(t) в моменты времени 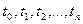примет значения меньшие соответственно 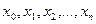, т.е.

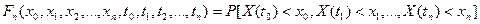. (6.1)

Если функция 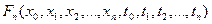имеет смешанную частную производную по аргументам 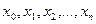, т.е.

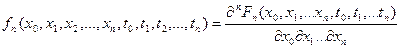, (6.2)

то она называется n – мерной плотностью вероятности случайного процесса.

Эти функции в зависимости от числа сечений позволяют получить наиболее полное описание случайного процесса. Однако для решения многих инженерных задач достаточно знать одномерный или двумерный закон распределения случайного процесса, т.е. 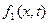или 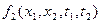. Если эти законы имеют нормальное распределение, то и случайный процесс X(t) также называют нормальным.