Передаточная функция.
ХАРАКТЕРИСТИКИ ДАТЧИКОВ
Может потребоваться несколько этапов преобразований, прежде чем входной сигнал, поступающий на датчик, превратится в выходной электрический сигнал. Для примера рассмотрим оптоволоконный датчик давления. Внешнее давление, действующее на датчик, вызывает деформацию волоконного световода, что в свою очередь приводит к изменению его показателя преломления, из-за чего меняются характеристики оптической линии передач и происходит модуляция плотности фотонов. Результирующий поток фотонов детектируется и преобразуется в электрический ток. Далее будут рассматриваться общие характеристики датчиков, вне зависимости от их физической природы и количества необходимых промежуточных этапов преобразований. При этом датчики будут представлены в виде «черных ящиков», где важными будут только соотношения между сигналами на их входах и выходах.
Передаточная функция.
Для каждого датчика можно вывести идеальное или теоретическое соотношение, связывающее сигналы на его входе и выходе. Если была бы возможность идеально спроектировать датчик, изготовить его из идеальных материалов и идеальными инструментами, при этом все работы выполнялись бы идеальными работниками, то сигнал на выходе такого датчика всегда бы соответствовал реальному значению внешнего воздействия. Выведенное идеальное соотношение между входным и выходным сигналом можно выразить в виде либо таблицы, либо графика, либо математического выражения. Это идеальное (теоретическое) выражение часто называют передаточной функцией. Передаточная функция устанавливает взаимосвязь между выходным электрическим сигналом датчика S и внешним воздействием s: S = f(s). Эта функция может быть как линейной, так и нелинейной (например, логарифмической, экспоненциальной или степенной). Во многих случаях передаточная функция является одномерной (т.е. связывает выходной сигнал только с одним внешним воздействием). Одномерную линейную функцию можно представить в виде выражения:
s = а + bs, (1)
где а - постоянная составляющая (т.е. значение выходного сигнала при нулевом входном воздействии), b - наклон прямой, который часто называют чувствительностью датчика.
Параметр S - эта та характеристика электрического сигнала, которую системы сбора данных воспринимают в качестве выходного сигнала датчика. В зависимости от свойств датчика это может быть амплитуда, частота или фаза.
Логарифмическая передаточная функция имеет вид:
s = а + blns,
экспоненциальная -
S = aeks,
степенная –
S = а0 + а1sk,
где k - постоянное число.
Однако датчик может иметь передаточную функцию, которую невозможно описать вышеприведенными аппроксимационными выражениями. В таких случаях применяются полиноминальные аппроксимации более высоких порядков.
Для нелинейных передаточных функций чувствительность не является константой, как это было в случае линейных зависимостей. Для каждого конкретного значения входного сигнала s0 ее можно определить в виде:

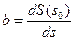
 (2)
(2)
Во многих случаях нелинейные датчики могут считаться линейными внутри ограниченного диапазона значений. Для более широкого диапазона значений нелинейная передаточная функция представляется в виде отрезков нескольких прямых линий. Это называется кусочно-линейной аппроксимацией. Для того, чтобы определить, может ли данная передаточная функция быть представлена в виде линейной зависимости, наблюдают за изменением выходных сигналов в линейной и реальной моделях при постепенном увеличении входного сигнала. Если разность сигналов не выходит за допустимые пределы, передаточную функцию данного датчика можно считать линейной.
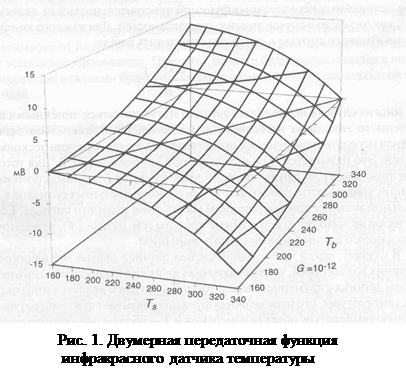
В случаях, когда на выходной сигнал датчика оказывают влияние несколько внешних воздействий, его передаточная функция становится многомерной. Примером датчика с двумерной передаточной функцией является инфракрасный датчик температуры. Его передаточная функция связывает две температуры (Тb - абсолютную температуру объекта измерения и Ts - абсолютную температуру поверхности сенсорного элемента) с выходным напряжением V:

 (3)
(3)
где G - константа. Из выражения видно, что зависимость между температурой объекта и выходным напряжением (передаточная функция) является не только нелинейной (параболой четвертого порядка), но она также зависит от температуры поверхности чувствительного элемента. Для определения чувствительности такого датчика по отношению к температуре объекта, надо взять частную производную от выражения (3):
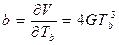
На рис. 1 передаточная функция (3) показана графически. Из рисунка видно, что каждое значение выходного напряжения однозначно определяется по двум входным температурам. Следует отметить, что, как правило, передаточные функции представляются в виде зависимости «выход от входа». Однако когда датчик используется для количественного определения внешнего воздействия, необходимо получить инверсную зависимость - «вход от выхода». При линейной передаточной функции получить обратную зависимость несложно. Но в случае присутствия в системе нелинейностей эта задача сильно усложняется, и во многих случаях аналитического выражения, пригодного для вычислений, получить не удается. Тогда снова привлекаются аппроксимационные методы.
Диапазон измеряемых значений.
Динамический диапазон внешних воздействий, который датчик может воспринять, называется диапазоном измеряемых значений (FS – full scale). Эта величина показывает максимально возможное значение входного сигнала, которое датчик может преобразовать в электрический сигнал, не выходя за пределы допустимых погрешностей. Для датчиков с очень широкой и нелинейной амплитудно-частотной характеристикой (АЧХ) динамический диапазон внешних воздействий часто выражается в децибелах, которые являются логарифмической мерой отношений либо мощности, либо напряжений. Всегда необходимо помнить, что децибелы выражают не абсолютные значения, а только отношения величин. Сигналы, отображенные в логарифмическом виде, имеют гораздо меньшие значения, чем исходные, что на практике в ряде случаев бывает очень удобно. Поскольку логарифмическая шкала является нелинейной, сигналы низкого уровня в ней представляются с большим разрешением, тогда как сигналы высокого уровня претерпевают большее сжатие. Другими словами, логарифмическая шкала для малых сигналов работает как микроскоп, а в случае больших сигналов - как телескоп. По определению децибел равен десяти логарифмам отношения мощности двух сигналов (см. таблицу 1), т.е.:
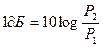 .
.
Исходя из этого, можно утверждать, что децибел в двадцать раз превышает логарифмы отношений силы, тока и напряжений, т.е.:
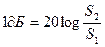 .
.
Таблица 1. Отношение между мощностью, силой (напряжением, током) и децибелами.
| Отношение мощности | 1,26 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 1010 | ||
| Отношение напряжения | 1,12 | 3,16 | 31,6 | 103 | 104 | 3*104 | 105 | ||||
| Децибелы |
Дата добавления: 2016-04-19; просмотров: 2461;
