Диапазон выходных значений

Диапазон выходных значений (FSO) - алгебраическая разность между электрически­ми выходными сигналами, измеренными при максимальном и минимальном внеш­нем воздействии. В эту величину должны входить все возможные отклонения от идеальной передаточной функции.

Точность

Точность - очень важная характеристика любого датчика. Правда, когда говорят о точности датчика, чаще всего подразумевают его неточность или погрешность из­мерений. Под погрешностью измерений, как правило, понимают величину мак­симального расхождения между показаниями реального и идеального датчиков. Считается, что измеренное значение соответствует реальному с определенной степенью достоверности.

Погрешность датчика можно также представить в виде разности между зна­чением, вычисленным по выходному сигналу датчика, и реальным значением по­данного входного сигнала. Например, рассмотрим линейный датчик перемеще­ний. В идеальном случае, если его чувствительность b равна 1 мВ/мм, при смеще­нии объекта на 1 мм напряжение на выходе должно измениться на 1 мВ. Однако на практике при перемещении объекта на расстояние S = 10 мм выходное напря­жение изменилось на 10,5 мВ, Т.е. S = 10,5 мВ. Преобразовав это значение при помощи инверсной передаточной функции, получим, что при таком напряже­нии перемещение объекта должно быть равным S_x = S/b = 10,5 мм, т.е. на 0,5 мм больше действительного. Вот эти 0,5 мм и являются погрешностью измерений. Следовательно, можно утверждать, что в пределах диапазона 10 мм абсолютная погрешность измерений данного датчика составляет 0,5 мм, а в относительных единицах она равна: (0,5 мм/10 мм)*100% = 5%. Если при отсутствии случайных ошибок каждый раз при повторении этого эксперимента будет наблюдаться по­грешность, равная 0,5 мм, говорят, что датчик в диапазоне 10 мм имеет система­тическую погрешность, равную 0,5 мм. Но, как правило, случайные ошибки все­гда присутствуют, поэтому на практике систематическая погрешность чаще всего представляется в виде среднего значения из множества экспериментальных зна­чений.

На рис. 2А показана идеальная или теоретическая передаточная функция. В реальной

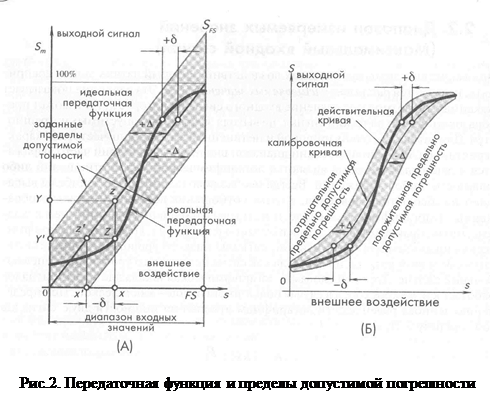
жизни любой датчик обладает теми или иными недостатками. Тол­стой линией на рисунке выделена одна из реальных передаточных функций, ко­торые не обязательно являются линейными и монотонными. Реальная функция почти никогда не совпадает с идеальной. Даже когда датчики изготавливаются в идентичных условиях, из-за разницы в материалах, в мастерстве работников, ошибок разработчиков, производственных допусков и т.п., их передаточные фун­кции всегда будут различаться друг от друга. Однако все они не должны выходить за пределы определенной зоны, лежащей в границах предельно допустимых по­грешностей, которые находятся от линии идеальной передаточной функции на расстоянии ±∆. Следовательно, разница между реальной и идеальной передаточ­ной функцией δ всегда должна быть меньше или равна ∆. Для примера рассмот­рим ситуацию, когда входной сигнал датчика равен х (рис. 2А). В идеальном случае при этом выходной сигнал должен быть равен Y, что соответствует точке z на передаточной функции. Вместо этого по реальной функции при значении х мы попадем в точку Z, и, следовательно, получим выходной сигнал, равный Y', соответствующий точке z'. Ha идеальной передаточной функции, которой, в свою очередь, должен соответствовать входной сигнал х'. Поскольку х' < х, погреш­ность измерений в данном случае будет равна - δ.

На точность датчиков влияют такие характеристики как: гистерезис, мертвая зона, параметры калибровки, повторяемость датчиков от партии к партии и вос­производимость погрешностей, которые будут рассмотрены далее. Предельно допустимые погрешности обычно соответствуют самым худшим рабочим характеристикам датчиков. Из рис. 2Б видно, что при более коррект­ном проведении калибровки (например, при проведении калибровки на боль­шем количестве точек), калибровочная кривая проходит ближе к реальным пере­даточным функциям, что означает повышение точности измерений. На практи­ке пределы допустимых погрешностей устанавливаются не вокруг идеальной пе­редаточной функции, а относительно калибровочной кривой. Допустимые пре­делы становятся меньше, если они не включают в себя погрешности, связанные с различиями датчиков от партии к партии, а также когда они относятся только к одному специально откалиброванному датчику. Все это повышает точность изме­рений, однако значительно повышает стоимость, из-за чего во многих ситуациях эти методы не могут быть применены.

Погрешность датчиков может быть представлена в следующих видах:

1. Непосредственно в единицах измеряемой величины (∆),

2. В процентах от значения максимального входного сигнала,

З. В единицах выходного сигнала.

В современных датчиках точность часто характеризуется величиной статистической ошибки измерений, учитывающей влияние как систематических, так и случайных погрешностей, и независящих от ошибок, допущенных при определении передаточных функций.

Калибровка

Если производственные допуски на датчик и допуски на интерфейс (схемы пре­образования сигналов) превышают требуемую точность системы, всегда необ­ходимо проводить калибровку. Например, требуется измерить температуру с точностью ±0.5 °С датчиком, по справочным данным обладающим погрешнос­тью ±1 °С. Это можно сделать только после проведения калибровки конкретного датчика, что необходимо для нахождения его индивидуальной передаточной функции, а также после проведения полной калибровки системы. В процессе проведения полной калибровки определяются коэффициенты, описывающие передаточную функцию всей системы в целом, включая датчик, интерфейсное устройство и АЦП. Математическое описание передаточной функции необхо­димо знать до начала проведения калибровки. В процессе калибровки не­обходимо определить коэффициенты передаточ­ной функции, проводя калибровочные измерения в нескольких точках в зависимости от вида передаточ­ной функции.

Для проведения калибровки датчиков важно иметь точные физические этало­ны, позволяющие моделировать соответствующие внешние воздействия. Напри­мер, при калибровке контактного датчика температуры его необходимо помещать либо в резервуар с водой, либо в «сухой колодец», в которых есть возможность точ­но регулировать температуру. При калибровке инфракрасных датчиков требуется наличие черного тела, а для калибровки гигрометров - набор насыщенных раство­ров солей, используемых для поддержания постоянной относительной влажности в закрытом контейнере и т.д. Отсюда ясно видно, что точность последующих изме­рений напрямую связана с точностью проведения калибровки.

Гистерезис

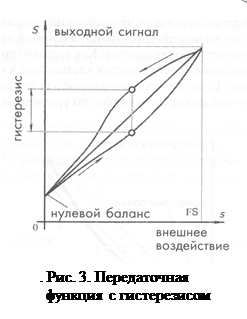
Гистерезис – это разность значений выходного сигнала для одного и того же входного сигнала, полученных при его возрастании и убывании (рис. 3). Например, пусть показания датчика перемещений при движении объекта слева направо отличаются на 20 мВ от его показаний при движении в той же самой точке справа налево. Если чувствительность датчика составляет 10 мВ/мм, ошибка гистерезиса будет равна 2 мм. Типичной причиной возникновения гистерезиса является трение и структурные изменения материалов.

Нелинейность

Нелинейность определяется для датчи­ков, передаточную функцию которых возможно аппроксимировать прямой линией (уравнение (1)). Под нелинейностью понимается максимальное откло­нение L реальной передаточной функ­ции от аппроксимирующей прямой ли­нии. Под термином «линейность» на самом деле понимается «нелинейность».

При проведении нескольких циклов калибровки выбирается худшее из получен­ных значений нелинейности. Нелинейность обычно выражается либо в процентах от максимального входного сигнала, либо в единицах измеряемых величин (на­пример, в кПа или ^оС). В зависимости от способа проведения аппроксимирующей линии различают несколько типов линеаризации. Один из способов – проведение прямой через конечные точки передаточной функции (рис. 4А). Для этого снача­ла определяются выходные значения, соответствующие наибольшему и наимень­шему внешним воздействиям, а потом через эти точки проводится прямая линия (линия 1). При такой линеаризации ошибка нелинейности минимальна в конеч­ных точках и максимальна где-то в промежутке между ними.

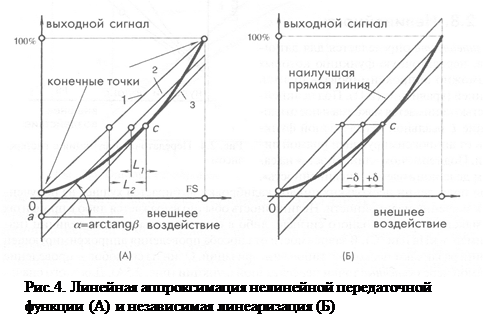
Другой способ линеаризации основан на применении метода наименьших квад­ратов (ли­ния 2 на рис. 4А). Для этого в широком диапазоне измеряемых величин (лучше в полном диапазоне) для ряда значений (n) внешних воздействий s измеря­ются выходные сигналы S. По­сле чего, применяя формулу линейной регрессии, определяют значения коэффициентов а и b:

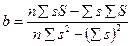
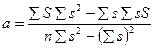
где Σ- это сумма n чисел.

На практике, в некоторых случаях, может потребоваться большая точность линеаризации в узком диапазоне входных сигналов. Например, медицинские тер­мометры должны обладать повышенной точностью в диапазоне 37 ^оС...38 ^оС. Вне этой зоны точность может быть несколько ниже. В этом случае калибровку прово­дят в узкой области, где требуется повышенная точность, после чего через калибро­вочную точку с проводится аппроксимирующая линия (линия 3 на рис. 4А). В результате такой процедуры наименьшее значение нелинейности достигается в зоне калибровочной точки, а ближе к концам диапазона измерения линейность значительно ухудшается. Как видно из рисунка, в данном методе аппроксимирую­щая линия часто является касательной к передаточной функции в точке калибров­ки с. Если известно выражение для реальной передаточной функции, наклон этой линии может быть найден по уравнению (2).

Метод независимой линеаризации часто называется «методом наилучшей прямой» (рис. 4Б). Он заключается в нахождении линии, проходящей посередине между дву­мя параллельными прямыми, располо­женными, как можно, ближе друг к другу и охватывающими все выходные значения реальной передаточной функции.

В зависимости от метода линеари­зации аппроксимирующие линии будут иметь разные коэффициенты а и b. Сле­довательно, значения нелинейности, полученные разными способами, могут серьезно различаться друг от друга.

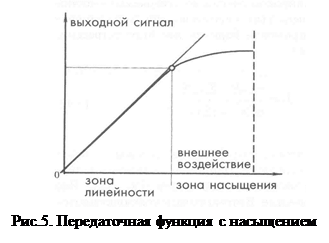
Насыщение

Каждый датчик имеет пределы рабочих характеристик. Даже если он считается линейным, при определенном уровне внешнего воздействия его выходной сигнал перестанет отвечать линейной зависимости. В этом случае говорят, что датчик вошел в зону нелинейности или в зону насыщения.

Воспроизводимость

Воспроизводимость – это способность датчика при соблюдении одинаковых условий выдавать идентичные результаты. Причинами плохой воспроизводимости результатов часто являются: тепловой шум, поверхностные заряды, пластичность материалов и т.д.

Мертвая зона

Мертвая зона – это нечувствительность датчика в определенном диапазоне входных сигналов. В пределах этой зоны выходной сигнал остается постоянным (часто равным нулю).