Где xn - диапазон измерений.

Чувствительность нельзя отождествлять с порогом чувствительности — наименьшим значением измеряемой величины, вызывающим заметное изменение показаний прибора.

Величину, обратную чувствительности, называют постоянной прибора

С = 1/S.

Как правило, выходным сигналом СИ является отсчет (показание) в единицах величины. В этом случае постоянная прибора С равна цене деления.

Вариация (гистерезис) — разность между показаниями СИ в данной точке диапазона измерения при возрастании и убывании измерений величины и неизменных внешних условиях:

Н= |х_в – x_у|

где х_в, х_у — значения измерений образцовыми СИ при возрастании и убывании величины х.

Следует иметь в виду, что, хотя вариация показаний СИ вызывается случайными факторами, сама она — не случайная величина.

Градуировочная характеристика - зависимость между выходным и входным сигналом СИ, полученная экспериментально. Она может быть представлена аналитически, графически или в виде таблицы.

Градуировочная характеристика может изменяться под воздействием внешних и внутренних причин. Например, при быстром изменении тока подвижная часть СИ, вследствие инерции, не успевает "следить" за изменением тока. Градуировочная характеристика в этом случае должна выражаться дифференциальным уравнением.

Основная MX СИ — погрешность СИ — есть разность между показаниями СИ и истинными (действительными) значениями ФВ.

Все погрешности СИ в зависимости от внешних условий делятся на основные и дополнительные.

Основная погрешность — это погрешность СИ при нормальных условиях эксплуатации.

Как правило, нормальными условиями эксплуатации являются: температура 293±5 К или 20±5 °С, относительная влажность воздуха 65+15% при 20 °С, напряжение в сети питания 220 В+10% с частотой 50 Гц±1%, атмосферное давление от 97,4 до 104 кПа, отсутствие электрических и магнитных полей (наводок).

В рабочих условиях, зачастую отличающихся от нормальных более широким диапазоном влияющих величин, при необходимости нормируется дополнительная погрешность СИ.

Существуют три способа нормирования основной погрешности СИ:

• нормирование пределов допускаемой абсолютной (±Δ) или приведенной погрешностей, постоянных во всем диапазоне измерения;

• нормирование пределов допускаемой абсолютной (±Δ) или относительной (±δ) погрешностей в функции измеряемой величины;

• нормирование постоянных пределов допускаемой основной погрешности, различных для всего диапазона измерений одного или нескольких участков.

В качестве предела допускаемой погрешности выступает наибольшая погрешность, вызываемая изменением влияющей величины, при которой СИ по техническим требованиям может быть допущено к применению. То же самое относится и к дополнительным погрешностям.

При этом исходят из следующих положений:

1) дополнительная погрешность имеет такой же вид, что и основная (абсолютная, относительная и приведенная);

2) дополнительные погрешности, вызванные различными влияющими факторами, должны нормироваться раздельно.

В общем виде суммарная абсолютная погрешность СИ при влияющих факторах имеет вид

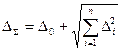
где Δ₀ — основная погрешность СИ; Δ_i — дополнительная погрешность, вызванная изменением i-го влияющего фактора.

Иногда дополнительную погрешность нормируютв виде коэффициента, указывающего, на сколько или во сколько раз изменяется погрешность при отклонении номинального значения. Например, указание, что температурная погрешность вольтметра составляет ±1% на 10°С, означает, что при изменении среды на каждые 10⁰С добавляется дополнительная погрешность 1%.

Вследствие сложности разделения дополнительных и основных погрешностей поверку СИ выполняют только при нормальных условиях (т. е. дополнительные погрешности исключены).

В соответствии с ГОСТ 8.401—80 для пределов допускаемой основной (и дополнительной) погрешностей предусмотрены различные способы выражения в виде абсолютной, относительной и приведенной погрешности.

Абсолютная погрешность — разность между показанием х СИ и действительным значением ха измеряемой величины

Δ =|x – x_д|

где в качестве х_д выступает либо номинальное значение (например, меры), либо значение величины, измеренной более точным (не менее чем на порядок, в 10 раз) СИ.

Абсолютная погрешность выражается в единицах измеряемой физической величины и может быть задана:

а) либо одним числом: Δ = ±а;

б) либо в виде линейной зависимости: Δ = ±bх; Δ=±(а+bx);

в) в виде функции Δ =f(х) или графика, таблицы.

Относительная погрешность.Поскольку абсолютная погрешность выражается в абсолютных единицах физической величины, то это не дает возможность сравнить СИ и измеряющие разные физические величины. Для этой цели можно использовать относительные погрешности, как отношение абсолютной погрешности к действительному х_д (x_d) значению, выраженные в процентах

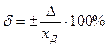
Эта формула показывает, что для одного и того же СИ δ уменьшается с ростом х_д и приближается к ∞ при х_д→0. То есть при измерении на начальном участке шкалы с начальной нулевой отметкой погрешности измерения могут быть сколь угодно велики. Поэтому в метрологии существует принцип запрета измерений на таких участках шкалы СИ.

Приведенная погрешность.Указание только абсолютной погрешности не позволяет сравнивать между собой по точности СИ с разным пределом измерений, а указание относительной погрешности также ограничено из-за непостоянства величины δ.

Поэтому получило большое распространение нормирование приведенной погрешности как отношение Δ к нормируемому значению x_N (в %):

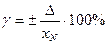
Нормирующее значение x_N выбирают в зависимости от вида и характера шкалы прибора.

Различают равномерные и неравномерные шкалы. Последние делятся на существенно неравномерные и степенные.

Под существенно неравномерной шкалой понимают шкалу с сужающимися делениями, на которой отметка, соответствующая полусумме начального и конечного значения рабочей части шкалы, расположена между 65 и 100% длины этой рабочей части.

Под степенной шкалой понимают шкалу с расширяющимися или сужающимися делениями, но не попадающими под определение существенно неравномерных.

Для равномерных и степенных шкал нормирующее значение x_N принимается равным:

• конечному значению рабочей части шкалы x_N= х_к если нулевая отметка — на краю или вне рабочей части шкалы

• сумме конечных значений шкалы (без учета знака), если нулевая отметка — внутри шкалы (x_N = 20+20 = 40; x_N= 20+40 = 60);

• номинальному значению х, если СИ предназначено для измерения отклонения измеряемой величины от номинального значения.

Для существенно неравномерных шкал нормирующее значение x_N принимается равным:

• длине шкалы. В этом случае, поскольку длина выражается в миллиметрах, то абсолютную погрешность надо выражать также в миллиметрах;

Специфическим видом погрешности цифровых СИ и дискретных преобразователей является погрешность квантования, которая вносится округлением значения измеряемой величины и номинального значения.

Поскольку измеряемая величина х может принимать случайные значения в интервале от +Δ до -Δ, то погрешность квантования есть случайная аддитивная статическая погрешность. Она не зависит ни от текущего значения х, ни от скорости изменения х во времени.

Погрешность от вариации (гистерезиса) Δ_H нормируется установлением предела H_p без учета знака допускаемой вариации выходного сигнала (показания) СИ.

Характеристику погрешности СИ, в том числе и в заданном интервале, нормируют установлением предела (положительного и отрицательного) Δ допускаемой погрешности совместно с Н_р.