Формулы для расчета результата эксперимента и его погрешности.
Как видно из формулы (5.9), зависимость Р = f(х – х0) является линейной. Следовательно, модуль Юнга следует рассчитывать по формуле:
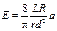 , ,
| (5.10) |
где а – угловой коэффициент прямой Р = f(х – х0), который находят по методу наименьших квадратов.
Доверительные границы модуля Юнга при этом равны:
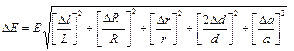
| (5.11) |
Погрешности измерения L и R, обозначенные соответственно ∆l и ∆R, определяются ценой деления линейки, ∆d следует вычислить по алгоритму прямых измерений, ∆r = 0.1 мм, ∆а рассчитывается по методу наименьших квадратов.
ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА ПО КРУЧЕНИЮ
Прежде чем приступить к работе, необходимо ознакомиться с введением по теме: "Деформация твердого тела"
Постановка экспериментальной задачи. Модуль сдвига можно определить, исследуя деформацию закручивания однородного круглого стержня. Если к круглому стержню радиуса r и длиной L приложить вращающий момент М, то угол закручивания φ определится соотношением
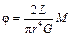 , ,
| (6.1) |
где G - модуль сдвига материала, из которого сделан стержень.
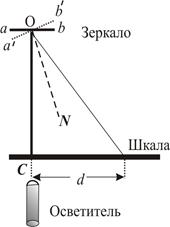
Описание экспериментальной установки. В данной работе для определения модуля сдвига используется установка, схематически изображенная на рис. 6.1
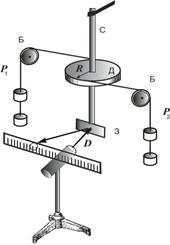
|
|
| Рис. 6.1 | Рис 6.2 |
Верхний конец вертикального стержня С жестко закреплен на стойке, а нижний соединен с диском Д. Момент M, закручивающий стержень, создают две скрепленные с ободом диска нити, перекинутые через блоки Б. К концам нитей подвешиваются одинаковые грузы P1 и P2 Конец стержня снабжен зеркальцем 3. Для определения угла закручивания надо луч осветителя направить на зеркальце и отраженный от него зайчик установить на нулевое деление шкалы, расположенной на расстоянии D от зеркальца. Из рис. 6.2 видно, что при повороте зеркальца на угол φ нормаль ON к новому положению зеркальца составит с прежним ее положением OC угол NOC = φ. Отраженный от зеркальца луч повернется на угол, равный 2φ. Как следует из рис. 6.2, 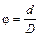 , где D – расстояние от зеркала до шкалы, а d -смещение зайчика по шкале. Отсюда угол поворота стержня в радианах определяется из формулы
, где D – расстояние от зеркала до шкалы, а d -смещение зайчика по шкале. Отсюда угол поворота стержня в радианах определяется из формулы
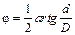 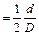 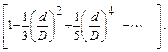
| (6.2) |
При вычислении угла φ по этой формуле членами разложения 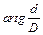 в ряд со степенями больше 2 можно пренебречь, ввиду их малости, тогда
в ряд со степенями больше 2 можно пренебречь, ввиду их малости, тогда
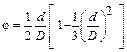 . .
| (6.3) |
Момент силы, действующий на стержень, равен M =PR, где P – суммарный вес грузов P1 и P2 , R – радиус диска Д (плечо вращающей силы). Тогда формула (13) примет вид
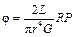 . .
| (6.4) |
В линейной зависимости φ = f(P) тангенс угла наклона tgθ прямой к оси абсцисс будет равен
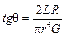 . .
| (6.5) |
Отсюда модуль сдвига материала стержня будет определяться через tgθ
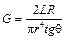 . .
| (6.6) |
Порядок выполнения работы
Устанавливают осветитель так, чтобы отраженный от зеркальца луч фокусировался на нулевом делении шкалы, шкала должна быть перпендикулярна лучу. На грузодержатели, левый и правый, кладут по одному грузу и определяют отклонение зайчика по шкале d1. Затем увеличивают нагрузку; кладут последовательно по 2, 3 и т.д. до 8 грузов на каждый грузодержатель, каждый раз определяя отклонение dn.
Но формуле (6.3) вычисляют значения углов поворота φ стержня для каждой суммарной нагрузки и строят график зависимости φ (угла поворота стержня в радианах) от Р (значения нагрузки в tgθ ньютонах).
Эту линейную зависимость обрабатывают по методу наименьших квадратов, определяют тангенс угла наклона прямой tgθ и его доверительные границы Δtgθ. Затем по формуле (6.6) определяют величину модуля сдвига G материала стержня.
Формулы для расчета погрешности результата экспериментаПогрешность определяют по следующей формуле:
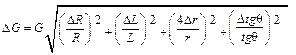 . .
| (6.7) |
Параметры установки:
| Стальной стержень | Латунный стержень |
| L = (128,7 ± 0,1) см R = (50,0 ± 0,1) мм 2r = (6,00 ± 0,01) мм | L = (128,8 ± 0,1) см R = (49,5 ± 0,1) мм 2r = (4,95 ± 0,01) мм |
Содержание отчета.
1. Общий вес грузов на грузодержателях выраженный в ньютонах (Н), отсчет по шкале осветителя d и расстояние D от зеркальца на установке до шкалы в миллиметрах.
2. Расчет величины 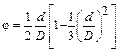 углов поворота стержня для всех нагрузок.
углов поворота стержня для всех нагрузок.
3. График зависимости угла поворота стержня в радианах от величины груза в ньютонах. Эта зависимость должна быть линейной. По графику необходимо определить приблизительное значение тангенса угла наклона этой прямой к оси абсцисс – tgθ.
4. Расчет по методу наименьших квадратов tgθ.
5. Расчет величины G по формуле (6.6).
6. Расчет погрешности модуля сдвига по формуле (6.7).
7. Окончательный результат модуля сдвига с погрешностью в системе СИ.
ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА КРУГЛОГО СТЕРЖНЯ МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Прежде чем приступить к работе, необходимо ознакомиться с введением по теме: “Деформация твердого тела”
Физическое обоснование эксперимента
Моментом силыотносительно некоторой точки О называется векторная величина М, определяемая выражением: 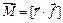 , где
, где 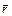 – радиус-вектор, проведенный из точки О в точку приложения силы
– радиус-вектор, проведенный из точки О в точку приложения силы 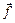
Моментом инерции системы материальных точек относительно оси С называется физическая величина равная сумме произведений их масс на квадраты расстояний до оси:I = Smiri2
К твердому телу, совершающему вращательные движения, может быть применен закон вращательного движения
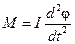 , ,
| (7.1) |
где М – момент возвращающей силы относительно оси вращения, I – момент инерции тела относительно той же оси, 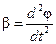 – угловое ускорение.
– угловое ускорение.
Если закрепить верхний конец круглого стержня, а нижний конец с прикрепленным к нему диском повернуть на угол φ и отпустить, то стержень может совершать крутильные колебания, при этом роль момента возвращающей силы будет выполнять момент силы упругости деформированного стержня.
Из уравнения (15) и третьего закона Ньютона видно, что момент силы равен
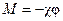 . .
| (7.2) |
Подставляя это значение в (7.1), получим дифференциальное уравнение, описывающее движение колеблющегося стержня
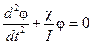 . .
| (7.3) |
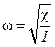 - круговая частота.
- круговая частота. Период таких колебаний равен соответственно:
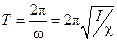 . .
| (7.4) |
Отсюда можно найти выражение для модуля сдвига G, если в (7.4) подставить значение величины χ из (14): 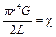 .
.
Окончательно имеем
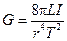 . .
| (7.5) |
Таким образом, для определения модуля сдвига G методом крутильных колебаний необходимо определить длину стержня L, его радиус r, момент инерции колеблющегося тела I и период его колебаний T.
Для расчета момента инерции рассматриваемого маятника используется дополнительное массивное кольцо K, момент инерции которого Io можно вычислить из геометрических размеров:
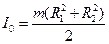 , ,
| (7.6) |
где R1 и R2 – внутренний и внешний радиусы кольца, m – его масса.
Если положить такое кольцо концентрически на диск (рис.7.1), то момент инерции получившейся системы будет равен (I + Io), т. к. момент инерции величина аддитивная. Период крутильных колебаний Т1 этой системы в соответствии с формулой (7.4) будет:
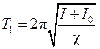 . .
| (7.7) |
Из выражений (7.7) и (7.4) получаем
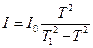 . .
| (7.8) |
Таким образом, определив момент инерции крутильного маятника, можно по формуле (7.5) можно определить модуль сдвига G.
Метод исследования и описание установки
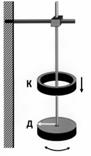
|
| Рис. 7.1 |
К нижнему концу зажатой вверху толстой проволоки, играющей роль круглого стержня, прикреплен горизонтальный диск (рис. 7.1). На этот диск может накладываться дополнительно массивное кольцо К. На диске Д нанесена стрелка, которая при положении равновесия должна находиться против неподвижной метки на стене.
Дата добавления: 2016-04-19; просмотров: 1416;

