Корреляционно-регрессионный анализ как основной метод изучения стохастических связей

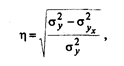
где σ_yx² — среднее квадратическое отклонение у от теоретических значений у_x; y_х определяется на основе уравнений регрессии; σ_y² — среднее квадратическое отклонение эмпирических (фактических) значений у.

В случае прямолинейной зависимости корреляционное отношение называется коэффициентом корреляции и обозначается буквой r.

Корреляционное отношение (коэффициент корреляции) принимает значения от 0 до 1:

если η (r) = 0, то связь между показателями отсутствует;

если η (r) = 1, то связь функциональная (детерминированная);

если η (r) — отрицательная величина, то связь между показателями обратная.

Алгоритм расчетов при корреляционном анализе связи парной корреляции состоит из ряда этапов.

Этап 1. Производится отбор наиболее важных существенных факторов, влияющих на результативный показатель. При отборе факторов учитываются причинно-следственные связи между показателями, причем все факторы должны быть количественно измеримы. Большую помощь при отборе факторов для корреляционной модели оказывают аналитические группировки, способ сравнения параллельных и динамических рядов, линейные графики. Отбор показателей для анализа и придание им статуса фактора или результативного значения осуществляются на основе знания экономических законов. Например, знание закона спроса и предложения помогает изучить влияние ценового фактора на изменение спроса. Отобранные для анализа показатели и результаты наблюдений за их изменением помещаются в таблицу, в которой факторные признаки располагаются в порядке возрастания или убывания, т.е. ранжируются.

Этап 2. Данные из таблицы наносятся на плоскость координат — строится корреляционное поле.

Этап 3. Производится обоснование формы связи:

• по форме корреляционного поля;

• путем визуального анализа ранжированного ряда.

Подобное обоснование является приблизительным и нуждается в дальнейшем уточнении с помощью ошибки аппроксимации.

Форма связи определяет дальнейшие действия корреляционного анализа.

Если связь носит прямолинейный характер, то рассчитывается коэффициент корреляции.

Если связь криволинейная, то прежде всего определяются теоретические значения у_x. С этой целью решается уравнение регрессии, описывающее связь между изучаемыми показателями. Затем рассчитывается корреляционное отношение.

Корреляционное отношение, или коэффициент корреляции, дает количественную оценку тесноты связи, характеризует силу влияния факторных признаков на результативные.

При прямолинейной форме связи коэффициент корреляции рассчитывается по формуле:

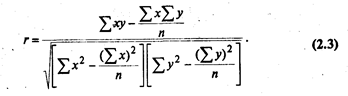
Коэффициент корреляции может быть представлен и как среднее значение произведений нормированных отклонений (t_x, t_y).

Нормированные отклонения определяются по формулам:

где σ_x, σ_у — средние квадратические отклонения:

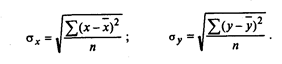
Если коэффициент корреляции возвести в квадрат, то получим коэффициент (индекс) детерминации, который показывает, чему равна доля влияния изучаемого фактора на совокупный показатель.

При значениях тесноты связи меньше 0,7 величина индекса детерминации d всегда будет меньше 50%. Это означает, что на долю вариации факторного признака х приходится меньшая доля по сравнению с другими признаками, влияющими на изменение результативного показателя. Синтезированные при таких условиях математические модели связи практического значения не имеют.

Если значения показателей тесноты связи более 0,7, выбирается уравнение регрессии, с помощью которого описывается форма связи между показателями.

Этап 4. Выбор и решение уравнения регрессии. Выбор конкретного уравнения регрессии, адекватно описывающего форму связи, является довольно сложной процедурой. В условиях использования ПЭВМ выбор адекватной модели осуществляется перебором решений, наиболее часто применяемых в анализе парной корреляции уравнений регрессии. Если форму связи сразу установить сложно, решают уравнения нескольких типов. Выбор адекватной модели производится на основе ошибки аппроксимации ε:

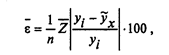
где 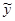_x — теоретическое значение, рассчитанное на основе выбранной модели.

Наибольшее значение ошибки аппроксимации свидетельствует о том, что оцениваемая модель дает наиболее адекватное описание формы взаимосвязи. Причем ошибка аппроксимации не должна превышать 0,2, или 20%.

Прямолинейное уравнение регрессии показывает равномерное нарастание результативного признака с увеличением факторного:

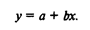
Коэффициент регрессии b несет основную смысловую нагрузку в уравнении регрессии. Он показывает, на сколько единиц в среднем изменяется результативный признак у с изменением на одну единицу факторного признака х. Эта всегда именованная величина b на графике показывает угол наклона прямой.

Свободный член а показывает начальную ординату, т.е. расстояние от начала координат до пересечения прямой с осью у.

Значения коэффициентов определяются методом наименьших квадратов. Он основан на предположении, что линия, выравнивающая эмпирические данные, должна проходить так, чтобы сумма квадратов отклонений от этой линии была наименьшей, т.е.

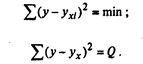
Подставим в выражение Q теоретическое значение результативного признака у_x = а + bх, получим

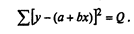
Q принимает минимальное значение, если частные производные

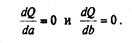
После дифференцирования получим

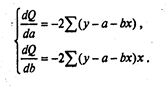
Приравняв обе части к 0 и умножив их на – , получим:

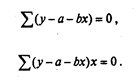
Суммируя каждый член уравнения в отдельности, получим:

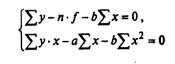
или

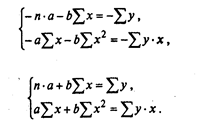
Криволинейная форма связи может быть представлена уравнением гиперболы, параболы, логарифмической функцией и т.д.:

а) уравнение гиперболы

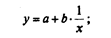
параметры а, b определяются на основе системы уравнений:

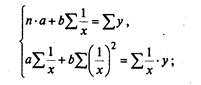
б) параболическая форма связи может описываться параболическим уравнением, например параболой 2-го порядка:

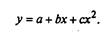
Расчет аргументов производится также на основе принципа наименьших квадратов, т.е.

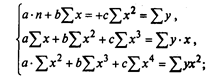
в) при логарифмической форме связи

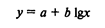
параметры уравнения определяются на основе системы уравнений:

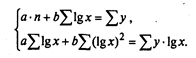
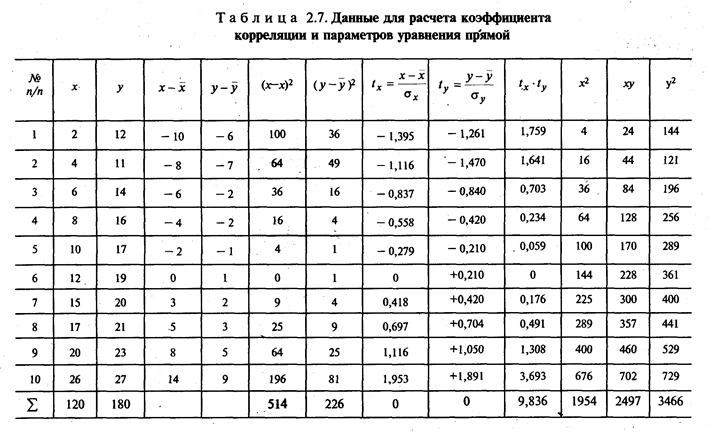
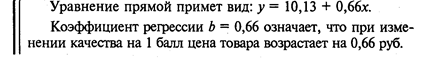
Этот условный пример показывает возможности метода в изучении зависимости между стохастическими показателями.

Математический аппарат регрессионного и корреляционного анализа оказался очень удобным для определения взаимозависимостей между различными величинами. Но наряду с простотой у этих видов анализа имеется существенный недостаток — исследуется только линейная зависимость между результирующим параметром и независимым фактором.

На практике значительно чаще встречаются многомерные зависимости, т.е. такие, в которых результирующий параметр зависит от многих факторов, и зависимости нелинейные.

Определение нелинейной корреляционной зависимости. Одним из способов нахождения зависимости является метод замены переменной. Этот метод довольно часто используется при решении различных математических задач. Он заключается в том, что независимый фактор заменяется некоторой функцией этого фактора, которая переводит нелинейную зависимость в разряд линейных.

Например, рассмотрим нелинейную зависимость вида у = х². Это не что иное, как парабола с вершиной в начале координат. Зависимость явно нелинейная. Чтобы убедиться в этом, достаточно посмотреть на график этой зависимости (рис. 2.3).

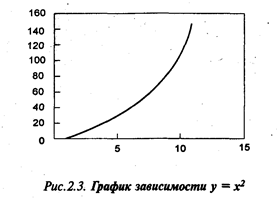
Сделаем замену переменной z = х². После подстановки в исходное уравнение получим зависимость вида у = z, которая уже является линейной. Для нее можно использовать весь математический аппарат регрессионного и корреляционного анализа, т.е. можно находить регрессионное уравнение, коэффициенты парной корреляции, ошибки и т. д.

Некоторые виды подстановок приведены в табл. 2.8.

Для нахождения лучшей подстановки можно использовать визуальный метод, когда «на глаз» определяется вид нелинейной зависимости, связывающей результирующий параметр и независимый фактор, а можно выбор наилучшей замены осуществлять, используя коэффициент корреляции. Та подстановка, у которой коэффициент корреляции является максимальным, и является наилучшей.

Метод множественной корреляции. Этот метод применяется в случаях когда результирующий показатель зависит от нескольких взаимно независимых факторов. При этом применяется уравнение множественной регрессии:

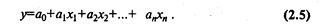
При n = 2 уравнение (2.5) превращается в обычное уравнение парной регрессии, при n = 3 это уравнение описывает плоскость, а при больших размерностях — гиперплоскость. Иногда эту гиперплоскость называют поверхностью отклика. Для определения коэффициентов регрессионного уравнения используется исходный статистический материал (табл. 2.9).

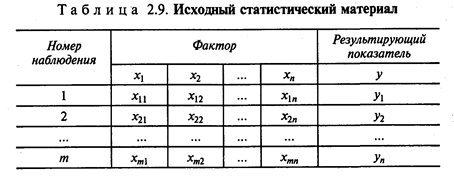
Необходимым условием для поиска коэффициентов является требование того, чтобы количество наблюдений было больше числа независимых факторов +1. Для определения коэффициентов регрессионного уравнения (2.5) удобнее всего использовать методы матричного исчисления. Для этого сделаем одно допущение, которое не меняет условия задачи. Будем считать, что в уравнении (2.5) свободный член a₀ всегда умножается на некоторый фиктивный фактор, имеющий постоянное значение, равное единице, т.е. имеем:

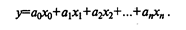
В исходной статистической матрице (табл. 2.12) должен появиться еще один столбец (X₀), все значения которого равны единице. Эту матрицу в дальнейшем будем обозначать буквой Х и называть расширенной матрицей независимых факторов:

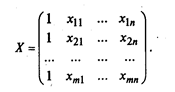
Введем также вектор результирующих параметров:

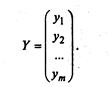
В этих обозначениях коэффициенты регрессионного уравнения (2.5) также можно представить в виде вектора:

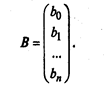
Тогда систему нормальных уравнений для отыскания неизвестных коэффициентов регрессионного уравнения (2.5) можно записать следующим образом:

где X^T — транспонированная расширенная матрица независимых факторов.

В расширенном виде матричное уравнение (2.5) запишется так:

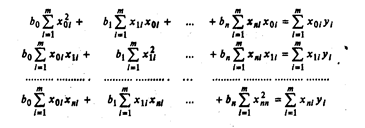
Если теперь обе части матричного уравнения умножить справа на матрицу, обратную Х^TX, то получим новое матричное уравнение:

где Е — единичная матрица.

Уравнение (2.7) и есть искомое для нахождения коэффициентов множественной регрессии.

Расчет взаимодействия между результирующим параметром и независимым фактором с помощью корреляционных функций. Несмотря на очевидные достоинства корреляционного метода анализа, у него есть существенный недостаток — поведение и результирующего показателя и независимого фактора должно изменяться одновременно. Если это условие не выполняется, то можно получить неадекватные выводы. Для устранения этого недостатка необходимо использовать корреляционные функции — автокорреляционную и взаимокорреляционную, формулы для расчета которых приведены ниже.

Автокорреляционная функция R_xx определяется следующим выражением:

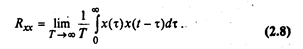
Взаимокорреляционная функция

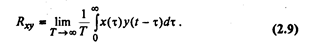
Определение временного сдвига (временного лага) двух переменных.На практике часто случается так, что реакция на какое-то возмущение в динамической системе (в качестве динамической системы может выступать экономическая система) следует не сразу, а через некоторый промежуток времени. Такой временной сдвиг в экономике называется временным лагом. С помощью взаимокорреляционной функции можно определить этот временной лаг. Значение независимой переменной, при котором наблюдается максимальное значение взаимокорреляционной функции, есть временной лаг (рис. 2.4).

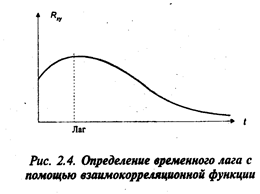
Учет временного сдвига при определении взаимозависимости результирующего параметра и независимого фактора позволяет получать более корректные выводы.

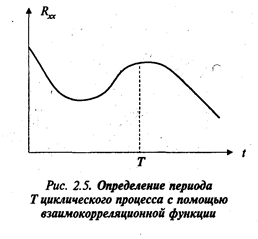
Определение периодических процессов. Встречающиеся иногда в практической деятельности периодические процессы также можно исследовать с помощью корреляционных функций, в данном случае — взаимокорреляционной функции. При этом максимальные значения взаимокорреляционной функции (рис. 2.5) будут соответствовать периодам исследуемого процесса.

Корреляционные функции позволяют более глубоко исследовать взаимозависимости различных переменных. Здесь приведены только самые общие понятия. При помощи этих функций можно исследовать различные классы зависимостей, в том числе и многомерные. Однако для применения этих методов необходимо использование информационных технологий, поскольку требуются значительные по объему вычисления.